题目内容
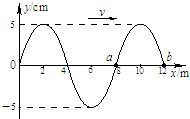
如图所示,a、b是水平绳上的两点,相距42cm,一列正弦波沿绳传播,方向从a到b,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,则此波的波长可能是( )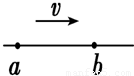
A.168cm
B.184cm
C.56cm
D.24cm
【答案】分析:根据a、b两点状态状态,结合波形,确定ab间距离与波长的关系,求出波长的通项,再得到波长的特殊值.
解答:解: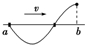 题中给出,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,如图所示,则ab间距离为
题中给出,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,如图所示,则ab间距离为 λ或1
λ或1 λ或2
λ或2 λ…,得到通式xab=(k+
λ…,得到通式xab=(k+ )λ(k=0,1,2…),由此可得到波长的可能值
)λ(k=0,1,2…),由此可得到波长的可能值
λ=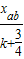 =
=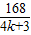 cm
cm
当k=0时,得到λ=56cm,此为波长最大值.
当k=1时,λ=24cm,
故选CD.
点评:本题知道两个质点的状态,通过画出波形,确定出两点距离与波长的关系是常用的思路.
解答:解:
 题中给出,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,如图所示,则ab间距离为
题中给出,每当a点经过平衡位置向上运动时,b点正好到达上方最大位移处,如图所示,则ab间距离为 λ或1
λ或1 λ或2
λ或2 λ…,得到通式xab=(k+
λ…,得到通式xab=(k+ )λ(k=0,1,2…),由此可得到波长的可能值
)λ(k=0,1,2…),由此可得到波长的可能值λ=
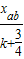 =
=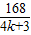 cm
cm当k=0时,得到λ=56cm,此为波长最大值.
当k=1时,λ=24cm,
故选CD.
点评:本题知道两个质点的状态,通过画出波形,确定出两点距离与波长的关系是常用的思路.

练习册系列答案
相关题目
 (模块3-4)如图所示,a与b是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为ra、rb,且ra>rb,则( )
(模块3-4)如图所示,a与b是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为ra、rb,且ra>rb,则( )
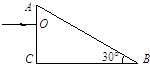
 (2010?宁河县一模)如图所示,a与b是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为ra、rb,且ra>rb,则( )
(2010?宁河县一模)如图所示,a与b是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为ra、rb,且ra>rb,则( )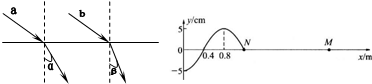
 (2006?广州二模)如图所示,a 与 b 是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为 ra、rb,若ra>rb,则( )
(2006?广州二模)如图所示,a 与 b 是两束平行的颜色不同的单色光,它们从空气中射入水中的折射角分别为 ra、rb,若ra>rb,则( )