Question

一个电荷量为－q，质量为m的小球，从光滑绝缘的斜面轨道的A点由静止下滑，小球恰能通过半径为R的竖直圆形轨道的最高点B而做圆周运动。现在竖直方向上加如图所示的匀强电场，且电场强度满足mg=2qE，若仍从A点由静止释放该小球，则（??? ）

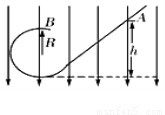
A．小球仍恰好能过B点

B．小球不能过B点

C．小球能过B点，且在B点与轨道之间压力不为零

D．小球到达B点的速度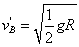

 

Answer 1

【答案】

AD

【解析】

试题分析：没有电场时，最高点速度设为v； 则 mg=m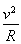;又根据机械能守恒定律

    mg（h-2R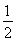）=mv2  ；解得h=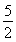R

    加上电场时，恰好过最高点需要的速度设为v′，则mg-qE=m，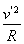

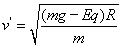
而由动能定理，得mg（h-2R）-qE（h-2R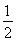）=mv′2，解得：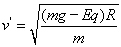

  说明小球仍恰好能过B点．故A正确，B错误．由以上分析可知，小球仍恰好过最高点，球与轨道间无作用力．故C错误；由于mg=2qE，所以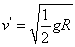，选项D正确。

考点：动能定理及牛顿定律的应用。