题目内容
质量为M、长为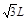 的杆水平放置,杆两端A、B系着长为3L的不可伸长且光滑的柔软绳,绳上套着一质量为m的小铁环。已知重力加速度为g,不计空气影响。
的杆水平放置,杆两端A、B系着长为3L的不可伸长且光滑的柔软绳,绳上套着一质量为m的小铁环。已知重力加速度为g,不计空气影响。
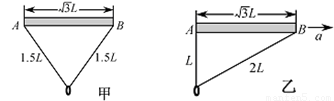
(1)现让杆和环均静止悬挂在空中,如图甲,求绳中拉力的大小;
(2)若杆与环保持相对静止,在空中沿AB方向水平向右做匀加速直线运动,此时环恰好悬于A端的正下方,如图乙所示。
①求此状态下杆的加速度大小a;
②为保持这种状态需在杆上施加一个多大的外力,方向如何?
(1)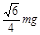 (1)①
(1)①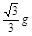 ②
②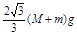 ,方向与水平方向成α=60°斜向上
,方向与水平方向成α=60°斜向上
【解析】(1)设平衡时绳中的拉力大小为T,绳与竖直方向间的夹角为θ,小球还受重力mg,如图1所示,根据共点力的平衡条件,在竖直方向上有:2Tcosθ=mg ①
由图中几何关系有:sinθ=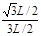 ②
②
又有sin2θ+cos2θ=1 ③
由①②③式联立解得:T=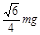
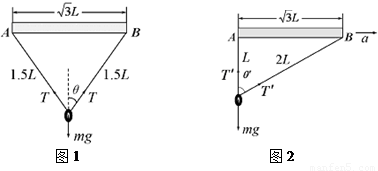
(2)①当杆与环保持相对静止呈图乙型随杆一起沿AB方向水平向右匀加速运动时,设此时绳中拉力为T′,绳倾斜部分与竖直方向间的夹角为θ′,根据牛顿第二定律可知,
在水平方向上有:T′sinθ′=ma ④
在竖直方向上有:T′+T′cosθ′-mg=0 ⑤
由图中几何关系有:sinθ′=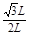 ⑥
⑥
由④⑤⑥式联立解得:a=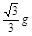 ⑦
⑦
②对环、杆整体,受重力(M+m)g和外力F作用,显然要保持整体水平向右加速运动,外力F应斜向上方,设F与水平方向间的夹角为α,根据牛顿第二定律可知,
在水平方向上有:Fcosα=(M+m)a ⑧
在竖直方向上有:Fsinα=(M+m)g ⑨
又有sin2α+cos2α=1 ⑩
由⑦⑧⑨⑩式联立解得:F=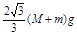 ,α=60°
,α=60°
【考点定位】本题主要考查了共点力平衡条件、牛顿第二定律的应用及整体法与隔离法的灵活使用问题,难度中等。

 出彩同步大试卷系列答案
出彩同步大试卷系列答案 如图所示,一个质量为m的圆环套在一根固定的水平直杆上,环与杆的动摩擦因数为μ,现给环一个向右的初速度,如果在运动过程中还受到一个方向始终竖直向上的力F的作用,已知力F的大小F=kv(k为常数,v为环的运动速度),则环在整个运动过程中克服摩擦力所做的功(假设杆足够长)可能为( )
如图所示,一个质量为m的圆环套在一根固定的水平直杆上,环与杆的动摩擦因数为μ,现给环一个向右的初速度,如果在运动过程中还受到一个方向始终竖直向上的力F的作用,已知力F的大小F=kv(k为常数,v为环的运动速度),则环在整个运动过程中克服摩擦力所做的功(假设杆足够长)可能为( )A、
| ||||||
B、
| ||||||
| C、0 | ||||||
D、
|
 一绝缘“?”形杆由两段相互平行的足够长的水平直杆PQ、MN和一半径为R的光滑半圆环MAP组成,固定在竖直平面内,其中MN杆是光滑的,PQ杆是粗糙的.现将一质量为m的带正电荷的小环套在MN杆上,小环所受的电场力为重力的
一绝缘“?”形杆由两段相互平行的足够长的水平直杆PQ、MN和一半径为R的光滑半圆环MAP组成,固定在竖直平面内,其中MN杆是光滑的,PQ杆是粗糙的.现将一质量为m的带正电荷的小环套在MN杆上,小环所受的电场力为重力的 .
.