题目内容
“嫦娥一号”于2009年3月1日下午4时13分成功撞月，从发射到撞落历时433天，标志我国一期探月工程圆满结束．其中，卫星发射过程先在近地圆轨道绕行3周，再长途跋涉进人近月圆轨道绕月飞行．若月球表面的重力加速度为地球表面重力加速度的
，月球半径为地球半径的
，据以上信息得（ ）
| 1 |
| 6 |
| 1 |
| 4 |
分析：抓住2点展开讨论：1、地球表面的重力加速度等于有引力加速度即重力和万有引力相等；2、近地绕月飞行和近月绕月飞行时重力提供圆周运动的向心力．
解答：解：A、根据近地（近月）飞行时，重力提供圆周运动的向心力可得：
mg=mR(
)2可得：周期T=
，所以周期之比
=
=
=
，故A正确；
B、根据近地（近月）飞行时，重力提供圆周运动的向心力可得：
mg=m
可得：v=
，所以飞行速度之比
=
=
≠
，故B错误；
C、根据近地（近月）飞行时，重力提供圆周运动的向心力可得：a向=g，所以
=
=
，故C错误；
D、在星球表面重力和万有引力相等可知：G
=mg，所以M=
，所以月球和地球的质量之比为：
=
=
×(
)2=
，故D错误．
故选A
mg=mR(
| 2π |
| T |
|
| T月 |
| T地 |
|
|
| ||
|
B、根据近地（近月）飞行时，重力提供圆周运动的向心力可得：
mg=m
| v2 |
| R |
| gR |
| v月 |
| v地 |
|
|
| 1 |
| 6 |
C、根据近地（近月）飞行时，重力提供圆周运动的向心力可得：a向=g，所以
| a月 |
| a地 |
| g月 |
| g地 |
| 1 |
| 6 |
D、在星球表面重力和万有引力相等可知：G
| mM |
| R2 |
| gR2 |
| G |
| M月 |
| M地 |
| ||||
|
| g月 |
| g地 |
| R月 |
| R地 |
| 1 |
| 96 |
故选A
点评：本题着重考查近地飞行的航天器由重力提供圆周运动的向心力；二是在地球表面重力和万有引力相等，由此根据万有引力列式进行计算即可．
练习册系列答案
阅读快车系列答案
相关题目
中国奔月探测卫星“嫦娥一号“已于10月24日下午6时05分准时成功发射升空．该卫星从地面发射后经多次变轨，进入高轨道，最后到达地月转移轨道，前后大约七到十天才进入距月球表面约200公里的预定月球轨道．下面关于探月卫星说法正确的是（ ）
| A、该卫星在地球轨道变轨过程中，需要加速才能进入高一轨道 | B、该卫星在月球上从高轨道到低轨道的过程中，需要减速制动 | C、该卫星在月球轨道运行的角速度大于在相同高度的地球轨道运动的角速度 | D、该卫星在绕月球做匀速圆周运动的过程中，卫星仍然处于完全失重状态 |
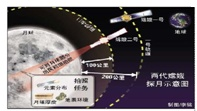“嫦娥二号”是我国月球探测第二期工程的先导星，目前已经完成各项技术攻关，将于今年10月份发射．“嫦娥二号”原本是“嫦娥一号”的备份卫星，因此两颗星在外形和重量上并没有太大差别．不过它的绕月飞行轨道将由“嫦娥一号”时的200公里高度降低到100公里，这样就能把月球看得更清楚．她们绕月球运动的示意图如右图所示（轨道视为圆周），则下列有关探月卫星的说法正确的是（ ）| A、“嫦娥二号”卫星绕月球运行的动能小于“嫦娥一号”卫星绕月球的动能 | B、“嫦娥二号”卫星在图示轨道上运行时的加速度大于月球表面的重力加速度 | C、“嫦娥二号”卫星所在位置的重力加速度比“嫦娥一号”所在位置的重力加速度大 | D、“嫦娥一号”卫星在绕月轨道上经过加速变轨可达到“嫦娥二号”的绕月轨道 |
