题目内容
 如图是传送带装运煤块的示意图,传送带长L=6m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮顶端与运煤车底板间的竖直高度H=l.8m,与运煤车车箱中心的水平距离x=1.2m.若以λ=100kg/s的速度把煤块放在传送带底端,煤块在传送带作用下的运动可视为由静止开始做匀加速直线运动,然后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.已知煤块在轮的最高点恰好水平抛出并落在车箱中心,全过程传送带与轮间不打滑,煤块视为质点,g取10m/s2,sin37°=0.6,cos37°=0.8;求:
如图是传送带装运煤块的示意图,传送带长L=6m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮顶端与运煤车底板间的竖直高度H=l.8m,与运煤车车箱中心的水平距离x=1.2m.若以λ=100kg/s的速度把煤块放在传送带底端,煤块在传送带作用下的运动可视为由静止开始做匀加速直线运动,然后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.已知煤块在轮的最高点恰好水平抛出并落在车箱中心,全过程传送带与轮间不打滑,煤块视为质点,g取10m/s2,sin37°=0.6,cos37°=0.8;求:(1)传送带匀速运动的速度v及主动轮和从动轮的半径R;
(2)动力轮带动传送带因传送煤块而增加的功率.
分析:(1)根据平抛运动的高度确定平抛的时间,再根据水平位移求出平抛运动的初速度.平抛运动的初速度等于传送带匀速运动的速度v.当煤块到达轮的最高点时对轮的压力为零,煤块做平抛运动,根据mg=m
求出从动轮的半径R.
(2)摩擦产生热为Q=f△x,根据能量守恒得动力轮做功等于摩擦产生热量和系统机械能增量,列出等式求解.
| v2 |
| R |
(2)摩擦产生热为Q=f△x,根据能量守恒得动力轮做功等于摩擦产生热量和系统机械能增量,列出等式求解.
解答:解:(l)由平抛运动的公式,得x=vt
H=
gt2
代入数据解得v=2m/s
要使煤块在轮的最高点做平抛运动,则煤块到达轮的最高点时对轮的压力为零,
由牛顿第二定律,得mg=m
代入数据得R=0.4m
故传送带匀速运动的速度v为2m/s,从动轮的半径R为0.4m
(2)设动力轮对传送带的功率为P,在时间t内有质量为m的煤块到达最高点,
动力轮做功为W,系统机械能增量为△E,摩擦产生热为Q,
则有W=Pt,m=λt
△E=mgLsinθ+
mv2
Q=μmgcosθ?△s
煤块相对于传送带的距离△s=s传-s煤
设煤块经过t0时间,速度达到传送带速度v,
根据运动学公式t0=
s煤=
s传=
根据牛顿第二定律
μmgcosθ-mgsinθ=ma
根据能量守恒得:W=Q+△E
解得P=7×103w
答:(1)传送带匀速运动的速度是=2m/s及主动轮和从动轮的半径是0.4m;
(2)动力轮带动传送带因传送煤块而增加的功率是7×103w.
H=
| 1 |
| 2 |
代入数据解得v=2m/s
要使煤块在轮的最高点做平抛运动,则煤块到达轮的最高点时对轮的压力为零,
由牛顿第二定律,得mg=m
| v2 |
| R |
代入数据得R=0.4m
故传送带匀速运动的速度v为2m/s,从动轮的半径R为0.4m
(2)设动力轮对传送带的功率为P,在时间t内有质量为m的煤块到达最高点,
动力轮做功为W,系统机械能增量为△E,摩擦产生热为Q,
则有W=Pt,m=λt
△E=mgLsinθ+
| 1 |
| 2 |
Q=μmgcosθ?△s
煤块相对于传送带的距离△s=s传-s煤
设煤块经过t0时间,速度达到传送带速度v,
根据运动学公式t0=
| v-0 |
| a |
s煤=
| v2 |
| 2a |
s传=
| v2 |
| a |
根据牛顿第二定律
μmgcosθ-mgsinθ=ma
根据能量守恒得:W=Q+△E
解得P=7×103w
答:(1)传送带匀速运动的速度是=2m/s及主动轮和从动轮的半径是0.4m;
(2)动力轮带动传送带因传送煤块而增加的功率是7×103w.
点评:解决本题的关键知道平抛运动的初速度等于传送带的速度,以及知道煤块先做匀加速运动再做匀速运动,最后做平抛运动.掌握功能关系得应用.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
 如图是利用传送带装运煤块的示意图,传送带足够长,煤块与传送带间的动摩擦因数μ=0.4,传送带与运煤车的车厢底板间的竖直高度H=1.8m,与车箱底板中心的水平距离x=1.2m.从传送带左端由静止释放的煤块(可视为质点)沿传送带先做匀加速直线运动,后随传送带一起做匀速运动,最后从右端水平抛出并落在车箱底板中心,取g=10m/s2,求:
如图是利用传送带装运煤块的示意图,传送带足够长,煤块与传送带间的动摩擦因数μ=0.4,传送带与运煤车的车厢底板间的竖直高度H=1.8m,与车箱底板中心的水平距离x=1.2m.从传送带左端由静止释放的煤块(可视为质点)沿传送带先做匀加速直线运动,后随传送带一起做匀速运动,最后从右端水平抛出并落在车箱底板中心,取g=10m/s2,求: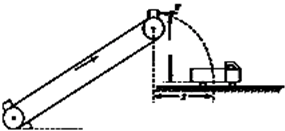
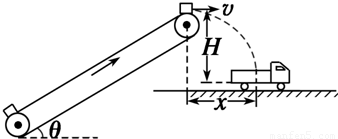 如图是传送带装运煤块的示意图,传送带长L=6m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮顶端与运煤车底板间的竖直高度H=l.8m,与运煤车车箱中心的水平距离x=1.2m.若以λ=100kg/s的速度把煤块放在传送带底端,煤块在传送带作用下的运动可视为由静止开始做匀加速直线运动,然后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.已知煤块在轮的最高点恰好水平抛出并落在车箱中心,全过程传送带与轮间不打滑,煤块视为质点,g取10m/s2,sin37°=0.6,cos37°=0.8;求:
如图是传送带装运煤块的示意图,传送带长L=6m,倾角θ=37°,煤块与传送带间的动摩擦因数μ=0.8,传送带的主动轮和从动轮半径相等,主动轮顶端与运煤车底板间的竖直高度H=l.8m,与运煤车车箱中心的水平距离x=1.2m.若以λ=100kg/s的速度把煤块放在传送带底端,煤块在传送带作用下的运动可视为由静止开始做匀加速直线运动,然后与传送带一起做匀速运动,到达主动轮时随轮一起匀速转动.已知煤块在轮的最高点恰好水平抛出并落在车箱中心,全过程传送带与轮间不打滑,煤块视为质点,g取10m/s2,sin37°=0.6,cos37°=0.8;求: