Question

一颗炮弹从倾角为θ的斜坡底端向着坡上发射，发射速度为v₀，则它的最大射程是多大？（不计空气阻力）

 

Answer 1

【答案】

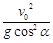（1－sinα）

【解析】如图所示，以炮弹发射点为原点O建立直角坐标系，设炮弹发射的角度为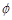（与x轴夹角）炮弹沿x方向的初速度为v₀cos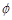，加速度是－gsinα，所以

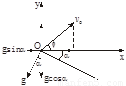
x=v₀tcos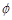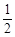－gt²sinα

在y方向，初速度为v₀sin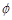，加速度为－gcosα，所以

y=v₀tsin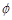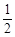－gt²cosα

求飞行时间：炮弹落地时y=0，即

v₀tsin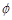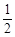－gt²cosα=0

所以t=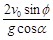，将t代入x中，则射程为

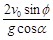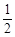x=vcosα－g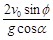（）²sinα

=

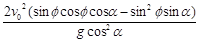
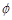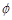因为2sincos=sin2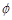，2sin²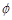=1－cos²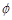

所以x=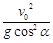［sin2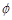cosα－（1－cos²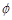）sinα］

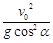=［sin（2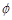+α）－sinα］

当sin（2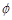+α）=1时，x有最大值x_max=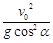（1－sinα）

这时的发射角必须满足

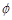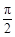2+α=　即=－.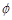

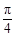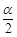思路分析：斜抛运动的有一种解法，把运动分解为沿初速度方向的匀减和垂直于初速度方向的匀加，同时也把重力加速度分解在两个分运动上，根据匀变速直线运动规律列出方程，利用数学方法求解。

试题点评：较为复杂的抛体运动，当做对曲线运动的加深理解即可，不是高考的重点。