题目内容
(2006?盐城二模)在匀强磁场中有一个静止的放射性C14原子核,它所放射的粒子与反冲核形成的轨迹是两个圆,圆的半径之比为l:2,那么C14的衰变方程是( )
分析:核衰变过程动量守恒,反冲核与释放出的粒子的动量大小相等,结合带电粒子在匀强磁场中圆周运动的半径公式可得小粒子与反冲核的电荷量之比,利用排除法可得正确答案
解答:解:原子核的衰变过程满足动量守恒,可得两带电粒子动量大小相等,方向相反,就动量大小而言有:
m1v1=m2v2
由带电粒子在匀强磁场中圆周运动的半径公式可得:
r=
所以,
=
=
审视ABCD四个选项,满足1:2关系的只有A
故选A
m1v1=m2v2
由带电粒子在匀强磁场中圆周运动的半径公式可得:
r=
| mv |
| qB |
所以,
| r1 |
| r2 |
| q2 |
| q1 |
| 1 |
| 2 |
审视ABCD四个选项,满足1:2关系的只有A
故选A
点评:原子核的衰变过程类比于爆炸过程,满足动量守恒,而带电粒子在匀强磁场中圆周运动的半径公式中的分子恰好是动量的表达式,要巧妙应用

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

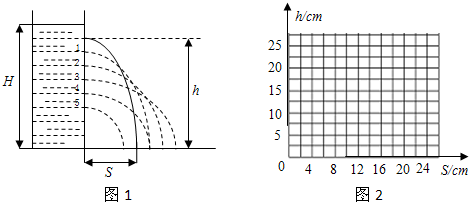
 (2006?盐城二模)如图所示,水平虚线L1、L2间的高度差h=5cm,L1的上方和L2的下方都存在垂直纸面向里的匀强磁场和竖直向上的匀强电场,下方磁场的磁感应强度是上方的
(2006?盐城二模)如图所示,水平虚线L1、L2间的高度差h=5cm,L1的上方和L2的下方都存在垂直纸面向里的匀强磁场和竖直向上的匀强电场,下方磁场的磁感应强度是上方的 (2006?盐城二模)竖直平面内有一光滑圆弧形轨道,O为最低点,A、B两点距0点的高度分别为h和4h,现从A点释放一质量为M的大物体,且每隔适当的时间从B点释放一质量为m的小物体,它们和大物体碰撞后都结为一体,已知M=100m,
(2006?盐城二模)竖直平面内有一光滑圆弧形轨道,O为最低点,A、B两点距0点的高度分别为h和4h,现从A点释放一质量为M的大物体,且每隔适当的时间从B点释放一质量为m的小物体,它们和大物体碰撞后都结为一体,已知M=100m,