题目内容
如图所示,一定质量的气体放在体积为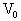 的容器中,室温为
的容器中,室温为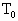 =300K,有一个光滑导热活塞C(不占体积)将容器分成A、B两室,B室的体积是A室体积的两倍,A室容器上连接有一个U形管(管内气体的体积忽略不计).两边水银柱高度差为76cm,右室容器连接有一个阀门K,可与大气相连通(外界大气压等于76cm汞柱)求:
=300K,有一个光滑导热活塞C(不占体积)将容器分成A、B两室,B室的体积是A室体积的两倍,A室容器上连接有一个U形管(管内气体的体积忽略不计).两边水银柱高度差为76cm,右室容器连接有一个阀门K,可与大气相连通(外界大气压等于76cm汞柱)求:
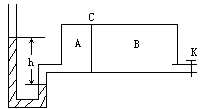
(1)将阀门K打开后,A室的体积变成多少?
(2)打开阀门K后将容器内的气体从300K分别加热到400K和500K,U形管内两边水银面的高度差各为多少?
解析:
|
(1)因 据玻意耳定律: 有: (2)设经等压变化到 据盖·吕萨克定律: 有:2V/300=
即此时活塞未到右端,U管内两边水银面无高度差. 设经等压变化到 据盖·吕萨克定律: 有:2V/300=
即此时活塞已到右端,U管内两边水银面有高度差.设此时气体的体积为 据理想气体状态方程: 有: 又:
h=0.8×76cm=60.8cm 被封气体(1)问中活塞最终停下来时,由于是导热活塞,初、末状态同温,此时判断一下活塞能否到达最右端是问题的关键.因(2)问中活塞从未到达至到达右端的过程是等压过程,到达右端后的过程是等容过程. [思路一]把第(1)问的末态作为第(2)问的初态,看在等压条件下温度为400K及500K时的体积与3V的关系,如<3V则无高度差,如>3V则用理想气体状态方程求出末状态气体的压强 [思路二]把第(1)问的末态作为第(2)问的初态,设第(2)问末态体积为3V,据盖·吕萨克定律求解末态温度 [思路三]把第(1)问的末态作为第(2)问的初态,先让气体等压达到3V求温度,再让气体等容升温至500K求压强 |
提示:
|
对一定质量的理想气体状态变化的问题,要注意始、末状态参量的确定,要注意状态参量与其它量的对应关系,尤其是压强状态参量与力的关系,本题中活塞能否到达最右端会影响到压强是否会发生变化.即本题的体积状态参量的变化中隐含着压强状态参量是否会发生变化的条件. 本题中活塞能否到达最右端是一个隐含条件,有了这一确定,其它状态参量也就容易确定了. |

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案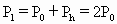 ,
,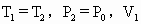 =V
=V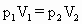
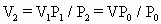 =2V
=2V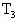 =400K时体积为
=400K时体积为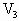
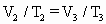
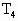 =500K时体积为
=500K时体积为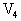
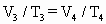
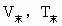 =500K,高度差为h,水银高度差产生的压强为
=500K,高度差为h,水银高度差产生的压强为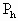 ,
,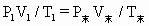
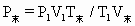 =2V×500
=2V×500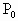 /3V×300=1.8
/3V×300=1.8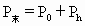
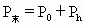
 与400K及500K比较判断,进而确定未态参量求解.
与400K及500K比较判断,进而确定未态参量求解. 如图所示,一定质量的小球,用一根细线悬挂于O点,在O正下方O'处有一钉子.将小球拉到P处后释放,当它摆到最低点P'时,悬线被钉子挡住.在绳与钉子相碰的瞬间,下列说法正确的是( )
如图所示,一定质量的小球,用一根细线悬挂于O点,在O正下方O'处有一钉子.将小球拉到P处后释放,当它摆到最低点P'时,悬线被钉子挡住.在绳与钉子相碰的瞬间,下列说法正确的是( ) 如图所示是一定质量的理想气体从状态A经B至C的P-
如图所示是一定质量的理想气体从状态A经B至C的P- (2013?惠州模拟)如图所示是一定质量的理想气体的P-T图线(P为气体压强,T为气体温度),当气体状态发生沿图线A到B的变化,下列说法中正确的是( )
(2013?惠州模拟)如图所示是一定质量的理想气体的P-T图线(P为气体压强,T为气体温度),当气体状态发生沿图线A到B的变化,下列说法中正确的是( ) (2012?潮州二模)如图所示是一定质量的理想气体的P-T图线(P为气体压强,T为气体温度),当气体状态沿图线由A到B的过程,下列说法中正确的是( )
(2012?潮州二模)如图所示是一定质量的理想气体的P-T图线(P为气体压强,T为气体温度),当气体状态沿图线由A到B的过程,下列说法中正确的是( ) 如图所示,一定质量的理想气体,沿状态A→B→C变化,则温度最高的是
如图所示,一定质量的理想气体,沿状态A→B→C变化,则温度最高的是