题目内容

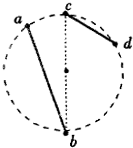如图所示，ab、cd是竖直平面内两根固定的光滑细杆，a、b、c、d位于同一圆周上，b点为圆周的最低点，c点为圆周的最高点，若每根杆上都套着一个小滑环（图中未画出），将两滑杆同时从a、c处由静止释放，用t1、t2分别表示滑环从a到b、c到d所用的时间，则（　　）
分析：设滑杆与竖直方向的夹角为α，根据牛顿第二定律和运动学公式列式，得出时间与α、圆周直径的关系式，进行分析．
解答：解：设滑杆与竖直方向的夹角为α，圆周的直径为D．
根据牛顿第二定律得：滑环的加速度为a=
mgcosα
m
=gcosα
滑杆的长度为 s=Dcosα
则根据s=
1
2
at2得，t=
2s
a
=
2Dcosα
gcosα
=
2D
g
，可见，时间t与α无关，故有t1=t2．
故选A
点评：本题关键从众多的杆中抽象出一根杆，根据牛顿第二定律求出加速度，再根据运动学公式求出时间表达式讨论．
练习册系列答案
相关题目
如图所示，AB和CD是足够长的平行光滑导轨，其间距为L，导轨平面与水平面的夹角为θ．整个装置处在磁感应强度为B，方向垂直于导轨平面向上的匀强磁场中，．AC端连有电阻值为R的电阻．若将一质量为M、电阻为r的金属棒EF垂直于导轨在距BD端s处由静止释放，在棒EF滑至底端前会有加速和匀速两个运动阶段．今用大小为F，方向沿斜面向上的恒力把棒EF从BD位置由静止推至距BD端s处，突然撤去恒力F，棒EF最后又回到BD端．（导轨的电阻不计）
（1）求棒EF下滑过程中的最大速度；
（2）求恒力F刚推棒EF时棒的加速度；
（3）棒EF自BD端出发又回到BD端的整个过程中，电阻R上有多少电能转化成了内能？
如图所示，ab、cd是竖直面内两根固定的光滑细杆，ab、cd两端位于相切的两个竖直圆周上，每根杆上都套着一个小滑环（图中未画出），两个滑环分别从a、c处释放（初速为0），用t1、t2依次表示滑环从a到b和从c到d所用的时间，则t1
等于
等于
t2．（填“大于、等于或小于”）
如图所示，AB和CD为半径为R=1m的1/4圆弧形光滑轨道，BC为一段长2m的水平轨道．质量为2kg的物体从轨道A端由静止释放，若物体与水平轨道BC间的动摩擦因数为0.1，试求：
（l）物体第1次沿CD弧形轨道可上升的最大高度．
（2）物体最终停下来的位置与B点的距离．
（3）如果物体的质量是4千克，则物体最终停下来的位置与B点的距离．
（2012?自贡模拟）如图所示，ab、cd为水平放置的足够长的平行光滑导轨，导轨间距l为0.5m，导轨左端连接一个4Ω的电阻R，将一根质量为0.2kg的金属棒ef垂直地放置导轨上，且与导轨接触良好．金属棒的电阻r大小为1Ω，导轨的电
阻不计．整个装置放在磁感强度B=2T的匀强磁场中，磁场方向垂直于导轨平面向下，现对金属棒施加一水平向右的拉力F使棒从静止开始向右运动．当棒的速度达到v0=3m/s后保持拉力的功率恒为5W，从此时开始计时（即此时t=0），已知从计时开始直至金属棒达到稳定速度的过程中电流通过电阻R做的功为6.72J．试解答以下问题：
（1）金属棒达到的稳定速度V是多少？
（2）金属棒从t=0开始直至达到稳定速度所需的时间是多少？
（3）试估算金属棒从t=0开始，直至达到稳定速度的过程中通过电阻R的电荷量的最大值是多少？
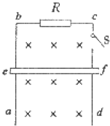精英家教网如图所示，ab、cd是固定在竖直平面内的足够长的金属框架，bc段接有一阻值为R的电阻，其余电阻不计，ef是一条不计电阻的金属杆，杆两端与ab和cd接触良好且能无摩擦下滑（不计空气阻力），下滑时ef始终处于水平位置，整个装置处于方向垂直框面向里的匀强磁场中，ef从静止下滑，经过一段时间后闭合开关S，则在闭合开关S后（　　）
A、ef的加速度大小不可能大于gB、无论何时闭合开关S，ef最终匀速运动时速度都相同C、无论何时闭合开关S，ef最终匀速运动时电流的功率都相同D、ef匀速下滑时，减少的机械能大于电路消耗的电能

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网