题目内容
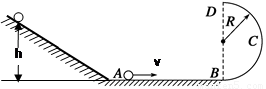
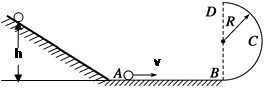
如图所示，质量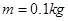
的金属小球从距水平面
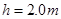的光滑斜面上由静止开始释放，运动到A点时无能量损耗，水平面
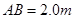的粗糙平面, 与半径为
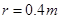的光滑的半圆形轨道BCD相切于B点，其中圆轨道在竖直平面内， D为轨道的最高点，小球恰能通过最高点D, 完成以下要求（
）
（1）小球运动到A点时的速度为多大？
（2）小球从A运动到B时摩擦阻力所做的功
（3）小球从B点飞出后落点E与A相距多少米？
（1）
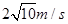（2）-1J（3）1.2m
解析试题分析：(1)、根据题意和图形可得；物体下落到A点时由动能定律得：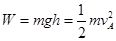
，
所以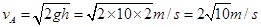
(2)物体运动到D点时: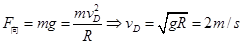
当物体由B运动到D点时机械能守恒定律得：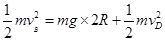
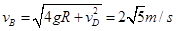
所以A到B时：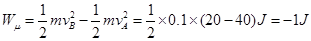
(3)物体从D点飞出后做平抛运动，故有：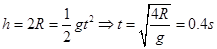
水平位移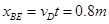
所以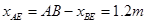
考点：动能定理、机械能守恒定律、平抛运动
点评：本题考查了动能定理、机械能守恒定律、平抛运动的综合应用，虽然有一定综合性，但比较基础
练习册系列答案
名师金手指领衔课时系列答案
相关题目
如图所示，光滑的金属导轨间距为L，导轨平面与水平面成α角，导轨下端接有阻值为R的电阻，质量为m的金属细杆ab与绝缘轻质弹簧相连静止在导轨上，弹簧劲度系数为k，上端固定，弹簧与导轨平面平行，整个装置处在垂直于导轨平面斜向上的匀强磁场中，磁感应强度为B．现给杆一沿轨道向下的初速度v0，杆向下运动至速度为零后，再沿轨道平面向上运动达最大速度，大小为v1，然后减速为零，再沿轨道平面向下运动…一直往复运动到静止（导轨与金属杆的电阻忽略不计）．试求：
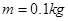的金属小球从距水平面
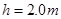的光滑斜面上由静止开始释放，运动到A点时无能量损耗，水平面
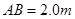的粗糙平面, 与半径为
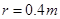的光滑的半圆形轨道BCD相切于B点，其中圆轨道在竖直平面内， D为轨道的最高点，小球恰能通过最高点D, 完成以下要求（
）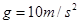