��Ŀ����
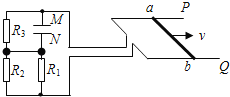
����Ŀ����ͼ�����費�Ƶ��㹻����ƽ�й⻬��������PX��QY���L=0.5m�������ӵ���R=2��������ƽ����б����=30��,��ǿ�ų���ֱ�ڵ���ƽ�����ϣ��Ÿ�Ӧǿ��B=1T������m=40g������R=0.5���Ľ�����MN���ڵ����ϣ�������ͨ����Եϸ���ڵ綯��ǣ���´Ӿ�ֹ��ʼ�˶�������ʱ��t1=2sͨ������x=1.5m���ٶȴﵽ�����������е�ѹ��ʾ��U0=8.0V��������ʵ��I0=0.6A��ʾ���ȶ����˶������н�����ʼ���뵼�촹ֱ��ϸ��ʼ���뵼��ƽ������ͬһƽ���ڣ��綯����Ȧ����r0=0.5����g=10m/s2.����
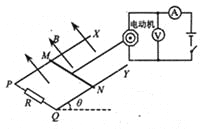
��1��ϸ�߶Խ����������Ĺ���P���
��2���Ӿ�ֹ��ʼ�˶���t1=2sʱ���ڣ�����R�ϲ���������QR�Ƕ��
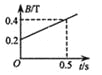
��3��������F����綯����ϸ�߷�����������MN��ʹ���������־�ֹ״̬���������������¶˾���Ϊd=1m�����ų�������ͼ���ɱ仯������F����ʱ��t�ı仯��ϵʽ��
���𰸡���1��0.3W����2��0.224J����3��F = 0.016t + 0.208��N��
��������
��1����������ת�����غ㣬��![]() ��� P = 0.3W
��� P = 0.3W
��2�����Ӿ�ֹ��ʼ�˶�����t1=2sʱ�䣬�������ٶȴﵽ������ʱΪvm���������е綯��ΪE������ΪI1���ܵ��İ�����ΪF����ϸ�ߵ�����ΪF������![]() ��
��![]()
F��= BI1L
P =F��vm
F�� = mgsin�� + F��
��� vm= 1m/s
�������Ӿ�ֹ��ʼ�˶����ﵽ����ٶȹ����У���������·�в���������ΪQ��������ת�����غ��
![]()
![]()
��� QR=0.224J
��3����ͼ��֪![]()
![]()
����tʱ�̣��ų��ĴŸ�Ӧǿ��ΪB'���������е綯��ΪE'������ΪI'���ܵ��İ�����Ϊ
F��'����
![]() ��T��
��T��
![]() ��
��![]()
F��' =B' I'L
![]() F��'
F��'
��� F = 0.016t + 0.208��N��