题目内容
在水平向右的匀强电场中，有一质量为m，带正电的小球，用长为l的绝缘细线悬挂于O点，当小球静止时细线与竖直方向夹角为θ，如图所示，现给小球一个初速度v0，使小球能在竖直平面内做圆周运动.试问：小球在做圆周运动的过程中，在哪一位置速度最小？速度最小时是多少？
解析：因为小球在B点时静止，所以小球在B点时小球受力平衡，对小球进行受力分析，小球受重力mg、拉力T和电场力F作用.当小球向上转时，拉力不做功，只有重力和电场力做功，并且重力和电场力始终不变，所以我们可以将小球所受的重力和电场力看作一个力，即这两个力的合力.这样我们就可以把这个问题转换成一个我们所熟悉的圆周运动来处理了，这个合力就相当于只有重力在小球上做功时的重力了，那么平衡点B就相当于小球运动的最低点，A点就相当于小球运动的最高点，即为小球速度最小的位置.
由动能定理：
×
mvA2-
mv02,
解得vA=
.
答案：A点速度最小；vA=
练习册系列答案
全能测控一本好卷系列答案
发散思维新课堂系列答案
相关题目
如图所示，一质量为m、带电量为q的小球，用绝缘细线悬挂在水平向右的匀强电场中，静止时悬线向左与竖直方向成θ角，重力加速度为g．
如图所示，质量相等的带电小球用绝缘细绳悬挂，小球间也用绝缘细绳连接，在水平向右的匀强电场中静止，球间作用力不计，现将其中一根悬线剪断，平衡时图中不可能出现的情况是（ ）
（2010?普陀区二模）如图所示，在水平向右的匀强电场中以竖直和水平方向建立直角坐标系，一带负电的油滴从坐标原点以初速度v0向第一象限某方向抛出，当油滴运动到最高点A（图中未画出）时速度为vt，试从做功与能量转化角度分析此过程，下列说法正确的是（ ）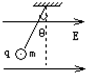
如图所示，一质量为m的带电小球，用绝缘细线悬挂在水平向右的匀强电场中，静止时悬线与竖直方向成θ角．已知电场强度为E，重力加速度为g
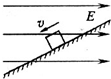如图所示，在水平向右的匀强电场中有一绝缘斜面，斜面上有一带电金属沿斜面滑下，已知在金属块滑下的过程中动能增加了12J，金属块克服摩擦力做功8.0J，重力做功24J，则以下判断正确的是（ ）