题目内容
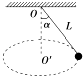
【题目】如图所示，光滑水平细杆MN、CD ， MN、CD在同一竖直平面内。两杆间距离为h ， N、C连线左侧存在有界的电场，电场强度为E。质量为m的带正电的小球P ， 穿在细杆上，从M端点由静止向N端点运动，在N、C连线中点固定一个带负电的小球，电荷量为Q。在匀强电场中做匀速圆周运动恰好回到C点，且小球P与细杆之间相互绝缘。
（1）求带正电的小球P的电荷量q 。
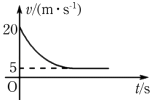
（2）求小球P在细杆MN上滑行的末速度v0
（3）求光滑水平细杆M、N两点之间的电势差。
【答案】
（1）
因带点小球做匀速圆周运动可得：
Eq=mg，所以 
（2）
库仑力提供向心力 
又因为h=2r
（3）
在细杆MN上由动能定理
【解析】 ①因带点小球做匀速圆周运动可得：
Eq=mg ， 所以
②库仑力提供向心力
又因为h=2r
③在细杆MN上由动能定理
【考点精析】利用带电微粒（计重力）在电场中的运动对题目进行判断即可得到答案，需要熟知带电颗粒:如液滴、油滴、尘埃、小球等，除有说明或明确的暗示以外，一般都不能忽略重力；由于带电粒子在匀强电场中所受电场力与重力都是恒力，因此可以用两种方法处理:①正交分解法;②等效“重力”法．
练习册系列答案
相关题目
