题目内容
如图所示,两根平行金属导轨间的距离为0.4 m,导轨平面与水平面的夹角为37°,磁感应强度为0.5 T的匀强磁场垂直于导轨平面斜向上,两根电阻值均为1 Ω、质量均为0.01kg的金属杆ab、cd水平地放在导轨上,并与导轨接触良好,杆与导轨间的动摩擦因数为0.3,导轨的电阻可以忽略。(sin37°=0.6,cos37°=0.8)

(1)用外力将ab固定在导轨上,使cd杆以1m/s的速度向上运动, 求ab杆中电流的大小和方向。
(2)撤去ab杆上的外力,为使ab杆能静止在导轨上,必须使cd杆以多大的速率沿斜面向上运动?
【答案】
(1)0.1A方向a→b(2)4.2
【解析】(1)(4分)cd杆运动产生的感应电动势为
ε=BLυ=0.5×0.4×1V=0.2V
电路中的电流I=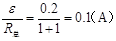 ,方向a→b
,方向a→b
(2)(8分)ab杆静止,摩擦力沿斜面向上最大时,安培力最小:mgsinθ=f+FAmin
FAmin= mgsinθ-f=0.1×0.6-0.3×0.1×0.8=0.036(N)
FAmin=BIminL=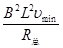 ,可求出
,可求出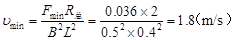
摩擦力沿斜面向下最大时,安培力最大:mgsinθ+f=FAmax
FAmax= mgsinθ+f=0.1×0.6+0.3×0.1×0.8=0.084(N)
可求出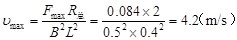
所以,为使ab杆能静止在导轨上,cd杆向上运动的速率范围为1.8m/s~4.2m/s。
本题考查了电磁感应与牛顿运动定律的综合问题,先根据法拉第电磁感应定律分析出感应电流,求出安培力,当安培力最小时有向下的运动趋势,摩擦力向上,反之摩擦力向下,列出两个平衡式求解

练习册系列答案
相关题目



 封一部分气体,活塞与容器壁间能无摩擦滑动,大气压恒为p0,容器的横截面积为S,密封气体的压强是 ,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,在此过程中密闭气体的内能增加 。
封一部分气体,活塞与容器壁间能无摩擦滑动,大气压恒为p0,容器的横截面积为S,密封气体的压强是 ,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,在此过程中密闭气体的内能增加 。 (2)(4分)沿x轴正方向传播的简谐横波在t=0时的波形如图所示,P、Q两个质点的平衡位置分别位于x=3.5m和x=6.5m处。在t1=0.5s时,质点P此后恰好第二次处于波峰位置;则t2= s时,质点Q此后第二次在平衡位置且向上运动;当t3=0.9s时,质点P的位移为__ ____cm。
(2)(4分)沿x轴正方向传播的简谐横波在t=0时的波形如图所示,P、Q两个质点的平衡位置分别位于x=3.5m和x=6.5m处。在t1=0.5s时,质点P此后恰好第二次处于波峰位置;则t2= s时,质点Q此后第二次在平衡位置且向上运动;当t3=0.9s时,质点P的位移为__ ____cm。  (3)(4分) 如图所示,透明介质球球心位于O,半径为R,光线DC平行于直径AOB射到介质的C点,DC与AB的距离H=
(3)(4分) 如图所示,透明介质球球心位于O,半径为R,光线DC平行于直径AOB射到介质的C点,DC与AB的距离H= 封一部分气体,活塞与容器壁间能无摩擦滑动,大气压恒为p0,容器的横截面积为S,密封气体的压强是 ,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,在此过程中密闭气体的内能增加 。
封一部分气体,活塞与容器壁间能无摩擦滑动,大气压恒为p0,容器的横截面积为S,密封气体的压强是 ,当气体从外界吸收热量Q后,活塞缓慢上升d后再次平衡,在此过程中密闭气体的内能增加 。 (2)(4分)沿x轴正方向传播的简谐横波在t=0时的波形如图所示,P、Q两个质点的平衡位置分别位于x=3.5m和x=6.5m处。在t1=0.5s时,质点P此后恰好第二次处于波峰位置;则t2=
s时,质点Q此后第二次在平衡位置且向上运动;当t3=0.9s时,质点P的位移为__ ____cm。
(2)(4分)沿x轴正方向传播的简谐横波在t=0时的波形如图所示,P、Q两个质点的平衡位置分别位于x=3.5m和x=6.5m处。在t1=0.5s时,质点P此后恰好第二次处于波峰位置;则t2=
s时,质点Q此后第二次在平衡位置且向上运动;当t3=0.9s时,质点P的位移为__ ____cm。  (3)(4分) 如图所示,透明介质球球心位于O,半径为R,光线DC平行于直径AOB射到介质的C点,DC与AB的距离H=
(3)(4分) 如图所示,透明介质球球心位于O,半径为R,光线DC平行于直径AOB射到介质的C点,DC与AB的距离H= R/2,若DC光线进入介质球后经一次反射再次回到介质球的界面时,从球内折射出的光线与入射光线平行,求介质的折射率。
R/2,若DC光线进入介质球后经一次反射再次回到介质球的界面时,从球内折射出的光线与入射光线平行,求介质的折射率。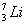 )俘获一个质量为m2的质子后衰变为两个
)俘获一个质量为m2的质子后衰变为两个 粒子,
粒子, 粒子以初动能E0与质量M的金核发生对心碰撞。若金核初时静止且自由,求
粒子以初动能E0与质量M的金核发生对心碰撞。若金核初时静止且自由,求