Question

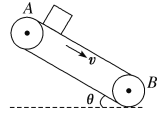
【题目】长为L的细线一端系一质量为m的小球，另一端固定在O点，现让小球在竖直平面内绕O点做圆周运动，A、B分别为小球运动过程中的最髙点与最低点位置，如图所示。某时刻小球运动到A位置时，细线对小球的作用力FA=mg，此后当小球运动到最低点B位置时，细线对小球的作用力FB=6mg，则小球从A运动到B的过程中（已知g为重力加速度，小球从A至B的过程所受空气阻力大小恒定），下列说法中正确的是

A.小球在最高点A位置时速度vA=

B.从A运动到B的过程中，小球所受的合外力方向总是指向圆心

C.从A运动到B的过程中，小球机械能减少mgL

D.从A运动到B的过程中，小球克服空气阻力做功为mgL

Answer 1

【答案】D

【解析】

A.小球在最高点的位置，由牛顿第二定律：

FA+mg= ，

解得：

vA=，

故A项错误；

B.小球从A运动到B的过程中，小球做变速圆周运动，合外力方向一般不指向圆心，故B项错误；

CD.小球在最低点B位置时：

FB-mg=，

解得：

vB=，

小球从A运动到B过程中，由动能定理得：

2mgL- Wf=-，

解得：

Wf=mgL，

所以此过程中，小球克服空气阻力做功为mgL，小球的机械能减小mgL，故C项错误，D项正确。