题目内容
2.某同学在“探究小车速度随时间变化的规律”的实验中,用打点计时器记录了被小车拖动的纸带的运动情况,在纸带上确定出A、B、C、D、E、F、G共7个计数点.其相邻点间的距离如图所示,每两个相邻的计数点之间还有4个打印点未画出.
(1)试根据纸带上各个计数点间的距离,计算出打下B点时小车的瞬时速度,并将这个速度值填入下表(要求保留3位有效数字).
| 速度 | vB | vC | vD | vE |
| 数值(m/s) | 0.479 | 0.560 | 0.640 |
分析 根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上B点时小车的瞬时速度大小.
解答 解:每两个相邻的测量点之间的时间间隔T=0.10s,
根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,
得:vB=$\frac{{x}_{AC}}{2T}$=$\frac{3.62+4.38}{2×0.1}×1{0}^{-2}$m/s=0.400m/s
根据匀变速直线运动的推论公式△x=aT2可以求出加速度的大小,
得:x4-x1=3a1T2
x5-x2=3a2T2
x6-x3=3a3T2
为了更加准确的求解加速度,我们对三个加速度取平均值
得:a=$\frac{1}{3}$(a1+a2+a3)
即小车运动的加速度计算表达式为:
a=$\frac{{x}_{6}+{x}_{5}+{x}_{4}-{x}_{3}-{x}_{2}-{x}_{1}}{9{T}^{2}}$
即:a=$\frac{(7.62+6.80+5.99)-(5.20+4.38+3.62)}{9×0.{1}^{2}}$×10-2m/s2=0.80m/s2
故答案为:(1)0.400;(3)0.80(0.70~0.90均给分).
点评 要学会应用匀变速直线的规律以及推论解答实验问题的能力,在平时练习中要加强基础知识的理解与应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
12. 如图所示,水平地面上有固定两块木板AB、BC,紧挨在一起,木板AB的长度是BC的三倍,一颗子弹以初速度v0从A端射入木板,到达 C端速度恰好为零,用的时间为t,子弹在木板中的运动可以看成是匀变速运动,则以下说法中正确的是( )
如图所示,水平地面上有固定两块木板AB、BC,紧挨在一起,木板AB的长度是BC的三倍,一颗子弹以初速度v0从A端射入木板,到达 C端速度恰好为零,用的时间为t,子弹在木板中的运动可以看成是匀变速运动,则以下说法中正确的是( )
 如图所示,水平地面上有固定两块木板AB、BC,紧挨在一起,木板AB的长度是BC的三倍,一颗子弹以初速度v0从A端射入木板,到达 C端速度恰好为零,用的时间为t,子弹在木板中的运动可以看成是匀变速运动,则以下说法中正确的是( )
如图所示,水平地面上有固定两块木板AB、BC,紧挨在一起,木板AB的长度是BC的三倍,一颗子弹以初速度v0从A端射入木板,到达 C端速度恰好为零,用的时间为t,子弹在木板中的运动可以看成是匀变速运动,则以下说法中正确的是( )| A. | 子弹从A到B的时间为$\frac{t}{2}$ | B. | 子弹从A到B的时间为$\frac{t}{4}$ | ||
| C. | 子弹到B点的速度为$\frac{{v}_{0}}{2}$ | D. | 子弹到B点的速度为$\frac{{v}_{0}}{4}$ |
13.对以a=5m/s2作匀加速直线运动的物体,下列说法正确的是( )
| A. | 在任意1s的末速度比初速度大5m/s | |
| B. | 第2s初的速度比第1s末的速度大5m/s | |
| C. | 任意1s末的速度比前1s的速度大5m/s | |
| D. | 第2s末的速度是第1s末的速度的5倍 |
17.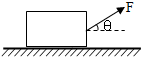 水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度保持不变,则( )
水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度保持不变,则( )
 水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度保持不变,则( )
水平地面上有一木箱,木箱与地面之间的动摩擦因数为μ(0<μ<1).现对木箱施加一拉力F,使木箱做匀速直线运动.设F的方向与水平面夹角为θ,如图,在θ从0逐渐增大到90°的过程中,木箱的速度保持不变,则( )| A. | F先减小后增大 | B. | F一直增大 | C. | F的功率变大 | D. | F的功率不变 |
7.甲、乙两物体由同一位置出发沿一直线运动,其速度-时间图象如图所示,下列说法正确的是( )


| A. | 甲做匀速直线运动,乙做匀变速直线运动 | |
| B. | 两物体分别在1s末和4 s末速度相同 | |
| C. | 乙在前2 s内做匀加速直线运动,2 s后做匀减速直线运动 | |
| D. | 2 s后,甲、乙两物体的速度方向相反 |
14.在一次跳伞训练中,伞兵从悬停在空中的直升机上跳出后,初速度v0>0,加速度a>0,下降过程中a值不断减小直至为零时,该伞兵的( )
| A. | 速度不断减小,位移先增大后减小 | |
| B. | 速度随时间均匀的增加 | |
| C. | 位移也随时间均匀增加 | |
| D. | 速度不断增大,当a=0时,速度达到最大,位移不断增大 |
11.有关电场强度的理解,下述说法正确的是( )
| A. | 由E=$\frac{F}{q}$可知,电场强度E跟放入的电荷q所受的电场力成正比 | |
| B. | 当电场中存在试探电荷时,电荷周围才出现电场这种特殊的物质,才存在电场强度 | |
| C. | 由E=$\frac{kq}{{r}^{2}}$可知,在离点电荷很远,r接近于无穷大,电场强度为零 | |
| D. | 电场强度是反映电场本身特性的物理量,与是否存在试探电荷无关 |
3. 如图,理想变压器的副线圈上通过输电线接有两个相同的灯泡L1和L2;输电线的等效电阻为R,开始时,电键K断开,当K断通时,以下说法正确的是( )
如图,理想变压器的副线圈上通过输电线接有两个相同的灯泡L1和L2;输电线的等效电阻为R,开始时,电键K断开,当K断通时,以下说法正确的是( )
 如图,理想变压器的副线圈上通过输电线接有两个相同的灯泡L1和L2;输电线的等效电阻为R,开始时,电键K断开,当K断通时,以下说法正确的是( )
如图,理想变压器的副线圈上通过输电线接有两个相同的灯泡L1和L2;输电线的等效电阻为R,开始时,电键K断开,当K断通时,以下说法正确的是( )| A. | 副线圈两端M、N的输出电压减小 | |
| B. | 副线圈输电线等效电阻R上的电压降减小 | |
| C. | 通过灯泡L1的电流增大 | |
| D. | 原线圈中的电流增大 |
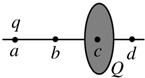 如图所示,一半径为R的圆盘上均匀分布着电荷量为Q的电荷,在垂直于圆盘且过圆心c的轴线上有a、b、d三个点,a和b、b和c、c和d间的距离均为R,在a点处有一电荷量为q(q>0)的固定点电荷.已知b点处的场强为零,则d点处场强的大小为$\frac{10kq}{{9R}^{2}}$(k为静电力常量).
如图所示,一半径为R的圆盘上均匀分布着电荷量为Q的电荷,在垂直于圆盘且过圆心c的轴线上有a、b、d三个点,a和b、b和c、c和d间的距离均为R,在a点处有一电荷量为q(q>0)的固定点电荷.已知b点处的场强为零,则d点处场强的大小为$\frac{10kq}{{9R}^{2}}$(k为静电力常量).