题目内容
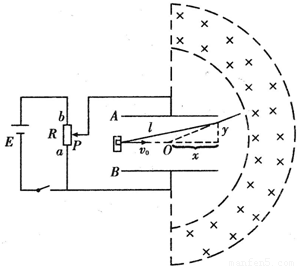 如图所示,两平行金属板A、B长度l=0.8m,间距d=0.6m.直流电源E能提供的最大电压为9×105V,位于极板左侧中央的粒子源可以沿水平方向向右连续发射比荷为q/m=l×107C/kg、重力不计的带电粒子,射人板间的粒子速度均为v=4×106m/s.在极板右侧有一个垂直纸面向里的匀强磁场,磁感应强度B=lT,分布在环带区域中,该环带的内外圆的圆心与两板间的中心重合于O点,环带的内圆半径Rl=
如图所示,两平行金属板A、B长度l=0.8m,间距d=0.6m.直流电源E能提供的最大电压为9×105V,位于极板左侧中央的粒子源可以沿水平方向向右连续发射比荷为q/m=l×107C/kg、重力不计的带电粒子,射人板间的粒子速度均为v=4×106m/s.在极板右侧有一个垂直纸面向里的匀强磁场,磁感应强度B=lT,分布在环带区域中,该环带的内外圆的圆心与两板间的中心重合于O点,环带的内圆半径Rl=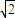 m.将变阻器滑动头由a向b慢慢滑动,改变两板间的电压时,带电粒子均能从不同位置穿出极板射向右侧磁场,且两板间电压最大时,对应的粒子恰能从极板右侧边缘穿出.
m.将变阻器滑动头由a向b慢慢滑动,改变两板间的电压时,带电粒子均能从不同位置穿出极板射向右侧磁场,且两板间电压最大时,对应的粒子恰能从极板右侧边缘穿出. (1)问从板间右侧射出的粒子速度的最大值vm是多少?
(2)若粒子射出电场时,速度的反向延长线与v所在直线交 于O′点,试用偏转运动相关量证明O′点与极板右端边缘的水平距离x=
 ,即O′与0重合,所有粒子都好像从两板的中心射 出一样.
,即O′与0重合,所有粒子都好像从两板的中心射 出一样. (3)为使粒子不从磁场右侧穿出,求环带磁场的最小宽度d.
【答案】分析:(1)由动能定理研究粒子从进极板到处极板的过程求解.
(2)根据类平抛运动的规律研究粒子在水平方向和竖直方向的运动,列出运动学等式结合几何关系证明.
(3)粒子进入磁场后做匀速圆周运动,画出粒子刚好不出磁场的临界轨迹图,根据洛伦兹力提供向心力结合几何关系求解.
解答:解:(1)由动能定理研究粒子从进极板到处极板的过程:
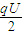 =
= mvm2-
mvm2- mv2
mv2
解出vm=5×106m/s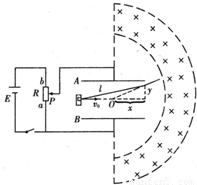
(2)证明:如图,设粒子在电场中的侧移为y,则
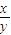 =
=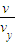
根据类平抛运动的规律研究粒子在水平方向和竖直方向的运动,
列出运动学等式:
l=vt y=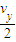 t
t
联立解得x=
(3)设环带外圆半径为R2,
所求d=R2-R1
粒子进入磁场后做匀速圆周运动,粒子刚好不出磁场的临界轨迹如图,
根据几何关系得:
R12+rm2=(R2-rm)2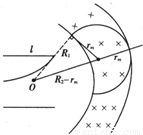
根据洛伦兹力提供向心力得:
qvmB=m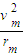
联立解得:d=(2-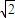 )m=0.586m
)m=0.586m
答:(1)从板间右侧射出的粒子速度的最大值是5×106m/s
(2)证明如上.
(3)环带磁场的最小宽度是0.586m.
点评:本题主要考查了带电粒子分别在电场和磁场中的运动情况,当两极间加上电压时,粒子做类平抛运动,根据类平抛运动规律求解问题.粒子在匀强磁场中的运动,要掌握住半径公式,画出粒子的运动轨迹后,几何关系就比较明显了.
(2)根据类平抛运动的规律研究粒子在水平方向和竖直方向的运动,列出运动学等式结合几何关系证明.
(3)粒子进入磁场后做匀速圆周运动,画出粒子刚好不出磁场的临界轨迹图,根据洛伦兹力提供向心力结合几何关系求解.
解答:解:(1)由动能定理研究粒子从进极板到处极板的过程:
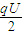 =
= mvm2-
mvm2- mv2
mv2解出vm=5×106m/s

(2)证明:如图,设粒子在电场中的侧移为y,则
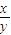 =
=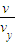
根据类平抛运动的规律研究粒子在水平方向和竖直方向的运动,
列出运动学等式:
l=vt y=
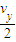 t
t 联立解得x=

(3)设环带外圆半径为R2,
所求d=R2-R1
粒子进入磁场后做匀速圆周运动,粒子刚好不出磁场的临界轨迹如图,
根据几何关系得:
R12+rm2=(R2-rm)2

根据洛伦兹力提供向心力得:
qvmB=m
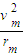
联立解得:d=(2-
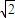 )m=0.586m
)m=0.586m 答:(1)从板间右侧射出的粒子速度的最大值是5×106m/s
(2)证明如上.
(3)环带磁场的最小宽度是0.586m.
点评:本题主要考查了带电粒子分别在电场和磁场中的运动情况,当两极间加上电压时,粒子做类平抛运动,根据类平抛运动规律求解问题.粒子在匀强磁场中的运动,要掌握住半径公式,画出粒子的运动轨迹后,几何关系就比较明显了.

练习册系列答案
相关题目
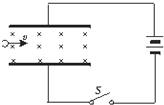 如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )
如图所示,两平行金属板水平放置,开始开关S合上使平行板电容器带电.板间存在垂直纸面向里的匀强磁场.一个不计重力的带电粒子恰能以水平向右的速度沿直线通过两板.在以下方法中,能使带电粒子仍沿水平直线通过两板的是( )| A、把两板间距离减小一半,同时把粒子速率增加一倍 | B、把两板的距离增大一倍,同时把板间的磁感应强度增大一倍 | C、把开关S断开,两板的距离增大一倍,同时把板间的磁感应强度减为一半 | D、把开关S断开,两板的距离减小一半,同时把粒子速率减小一半 |
 如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )
如图所示,两平行金属板间有一匀强电场,板长为L,板间距离为d,在 板右端L处有一竖直放置的光屏M,一带电荷量为q,质量为m的质点从两板中央射入板间,最后垂直打在M屏上,则下列结论正确的是( )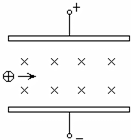 如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( )
如图所示,两平行金属板中有相互垂直的匀强电场和匀强磁场,带正电的粒子(不计粒子的重力)从两板中央垂直电场、磁场入射.它在金属板间运动的轨迹为水平直线,如图中虚线所示.若使粒子飞越金属板间的过程中向上板偏移,则可以采取下列的正确措施为( ) 如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( )
如图所示,两平行金属板的间距等于极板的长度,现有重力不计的正离子束以相同的初速度v0平行于两板从两板正中间射入.第一次在两极板间加恒定电压,建立场强为E的匀强电场,则正离子束刚好从上极板边缘飞出.第二次撤去电场,在两板间建立磁感应强度为B、方向垂直于纸面的匀强磁场,正离子束刚好从下极板边缘飞出,则E和B的大小之比为( ) 如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=
如图所示,两平行金属板间电场是匀强电场,场强大小为1.0×104V/m,A、B两板相距1cm,C点与A相距0.4cm,若B接地,则A、C间电势差UAC=