Question

（10分）如图所示，AB是一段位于竖直平面内的弧形轨道，高度为h，末端B处的切线沿水平方向。一个质量为m的小物体P（可视为质点）从轨道顶端处A点由静止释放，滑到B点时以水平速度v飞出，落在水平地面的C点，其轨迹如图中虚线BC所示。已知P落地时相对于B点的水平位移OC=l，重力加速度为g，不计空气阻力的作用。

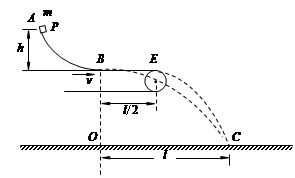
（1）请计算P在弧形轨道上滑行的过程中克服摩擦力所做的功；
（2）现于轨道下方紧贴B点安装一水平传送带，传送带右端E轮正上方与B点相距。先将驱动轮锁定，传送带处于静止状态。使P仍从A点处由静止释放，它离开B点后先在传送带上滑行，然后从传送带右端水平飞出，恰好仍落在地面上C点，其轨迹如图中虚线EC所示。若将驱动轮的锁定解除，并使驱动轮以角速度ω顺时针匀速转动，再使P仍从A点处由静止释放，最后P的落地点是D点（图中未画出）。已知驱动轮的半径为r，传送带与驱动轮之间不打滑，且传送带的厚度忽略不计。求：
①小物块P与传送带之间的动摩擦因数；
②若驱动轮以不同的角速度匀速转动，可得到与角速度ω对应的OD值，讨论OD的可能值与ω的对应关系。

Answer 1

（1）；
（2）①；
②当0﹤ω﹤时，OD=l；当ω﹥时，OD=（；当﹤ω﹤时，OD=。

试题分析：（1）小物块从A到B的过程中有重力和摩擦力对其做功，
故根据动能定理有：（2分）
解得（1分）
（2）① 需要先求出物块在E点的速度；
没有安装传送带时，小物块从B到C的过程，做平抛运动，水平方向有l=vt；
安装传送带后，小物块从E到C的过程沿水平方向有l/2=v_Et，二者的竖直高度相等，落下时所用的时间相等，故联立以上两个方程，解得v_E=（1分）
设小物块与传送带之间的动摩擦因数为μ，小物块从B到E的过程，根据动能定理有
- （2分） 
解得（1分）
②（a）当传送带的速度0﹤v_带=ωr﹤v_E，
即0﹤ω﹤时，物体在传送带上一直做匀减速运动，物体离开传送带时的速度为v_E，则OD=l…（1分）
（b）如果传送带的速度较快，物体在传送带上一直加速而未与传送带共速，则物体的加速度始终为a=设物体离开传送带时的速度为v_max，
根据运动学公式有解得v_max=
当传送带的速度v_带=ωr﹥，
即ω﹥时，物体离开传送带点时的速度为v_max，
则OD=+t=（…（1分）
（c）当传送带的速度v_E﹤v_带=ωr﹤v_max，
即﹤ω﹤时，物体离开传送带点时的速度为v_带=ωr，则OD=+ωrt=…（1分）