题目内容
9.某同学利用如图甲所示的实验装置,运用牛顿第二定律测量滑块的质量M.主要步骤为:
A.调整长木板倾角,当钩码的质量为m0时滑块沿木板恰好向下做匀速运动.
B.保持木板倾角不变,撤去钩码m0,将滑块移近打点计时器,然后释放滑块,滑块沿木板向下做匀加速直线运动,并打出点迹清晰的纸带如图乙所示(已知打点计时器每隔0.02s打下一个点).
请回答下列问题:
(1)打点计时器在打下B点时滑块的速度υB=1.38m/s;
(2)滑块做匀加速直线运动的加速度a=3.88m/s2;
(3)滑块质量M=$\frac{{m}_{0}g}{a}$(用字母a、m0、当地重力加速度g表示).
分析 (1)根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上B点时小车的瞬时速度大小;
(2)根据匀变速直线运动的推论公式△x=at2可以求出加速度的大小;
(3)应用牛顿第二定律可以求出滑块的质量.
解答 解:由图示纸带可知,两个相邻两个计数点间还有1个点,计数点间的时间间隔t=2T=0.04s,
(1)根据匀变速直线运动中时间中点的速度等于该过程中的平均速度,可以求出打纸带上B点时小车的瞬时速度大小.
vB=$\frac{{x}_{AC}}{2t}$=$\frac{0.0520+0.0584}{2×0.04}$=1.38m/s;
(2)根据匀变速直线运动的推论公式△x=at2可以知,加速度的大小:
a=$\frac{{x}_{CD}-{x}_{AB}+{x}_{DE}-{x}_{BC}}{4{t}^{2}}$=$\frac{0.0645-0.0520+0.0707-0.0584}{4×0.0{4}^{2}}$=3.88m/s2.
(3)滑块做匀速运动时受力平衡作用,由平衡条件得:m0g=Mgsinθ-f,撤去m0时滑块做匀加速直线运动时,
受到的合外力:F合=Mgsinθ-f,由牛顿第二定律得:F合=Ma,解得:M=$\frac{{m}_{0}g}{a}$.
故答案为:(1)1.38;(2)3.88;(3)$\frac{{m}_{0}g}{a}$.
点评 本题考查了牛顿第二定律的应用,应用匀变速直线运动的推论、牛顿第二定律即可解题,要熟练掌握基础知识,在平时练习中要加强基础知识的理解与应用.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
19. 如图为某小型水电站的电能输送示意图.已知发电机的输出电压为240V,输电线的总电阻R=16Ω,降压变压器T2的原、副线圈匝数之比为4:1,电阻R0=11Ω.若T1、T2均为理想变压器,T2的副线圈两端电压表达式为u=220$\sqrt{2}$sin 100πt V,下列说法正确的是( )
如图为某小型水电站的电能输送示意图.已知发电机的输出电压为240V,输电线的总电阻R=16Ω,降压变压器T2的原、副线圈匝数之比为4:1,电阻R0=11Ω.若T1、T2均为理想变压器,T2的副线圈两端电压表达式为u=220$\sqrt{2}$sin 100πt V,下列说法正确的是( )
 如图为某小型水电站的电能输送示意图.已知发电机的输出电压为240V,输电线的总电阻R=16Ω,降压变压器T2的原、副线圈匝数之比为4:1,电阻R0=11Ω.若T1、T2均为理想变压器,T2的副线圈两端电压表达式为u=220$\sqrt{2}$sin 100πt V,下列说法正确的是( )
如图为某小型水电站的电能输送示意图.已知发电机的输出电压为240V,输电线的总电阻R=16Ω,降压变压器T2的原、副线圈匝数之比为4:1,电阻R0=11Ω.若T1、T2均为理想变压器,T2的副线圈两端电压表达式为u=220$\sqrt{2}$sin 100πt V,下列说法正确的是( )| A. | 发电机中的电流变化频率为100 Hz | |
| B. | 升压变压器T1的原、副线圈匝数之比为1:4 | |
| C. | 升压变压器T1的输入功率为4800 W | |
| D. | 若R0的电阻减小,发电机的输出功率也减小 |
17.如图为a、b两物体同时开始运动的图象,下列说法正确的是( )


| A. | 若图象为位置-时间图象,则两物体在M时刻相遇 | |
| B. | 若图象为速度-时间图象,则两物体在M时刻相距最远 | |
| C. | 若图象为加速度-时间图象,则两物体在M时刻速度相同 | |
| D. | 若图象为作用在两物体上的合力-位移图象,则两物体在M位移内动能增量相同 |
14.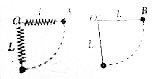 如图所示,长度为1的轻弹赞和长度为L(L>0)的轻绳.一端分别固定在同一高度的O点和O′点.另一端各系一个质量为m的小球A、B,把它们拉成水平状态,如图甲和乙,这时弹簧未伸长,由静止释放,到最低点,弹簧的长度也等于L(在弹性限度内),这时A、B两球在最低点的速度分别为vA和vB,则( )
如图所示,长度为1的轻弹赞和长度为L(L>0)的轻绳.一端分别固定在同一高度的O点和O′点.另一端各系一个质量为m的小球A、B,把它们拉成水平状态,如图甲和乙,这时弹簧未伸长,由静止释放,到最低点,弹簧的长度也等于L(在弹性限度内),这时A、B两球在最低点的速度分别为vA和vB,则( )
 如图所示,长度为1的轻弹赞和长度为L(L>0)的轻绳.一端分别固定在同一高度的O点和O′点.另一端各系一个质量为m的小球A、B,把它们拉成水平状态,如图甲和乙,这时弹簧未伸长,由静止释放,到最低点,弹簧的长度也等于L(在弹性限度内),这时A、B两球在最低点的速度分别为vA和vB,则( )
如图所示,长度为1的轻弹赞和长度为L(L>0)的轻绳.一端分别固定在同一高度的O点和O′点.另一端各系一个质量为m的小球A、B,把它们拉成水平状态,如图甲和乙,这时弹簧未伸长,由静止释放,到最低点,弹簧的长度也等于L(在弹性限度内),这时A、B两球在最低点的速度分别为vA和vB,则( )| A. | vA>vB | B. | vA<vB | C. | vA=vB | D. | 无法判定 |
1. 有a、b、c、d四颗地球卫星,a还未发射,在地球赤道上某处放置,b在地球表面附近的近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星.各卫星排列位置如图所示,则四颗卫星中,向心加速度最大的是( )
有a、b、c、d四颗地球卫星,a还未发射,在地球赤道上某处放置,b在地球表面附近的近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星.各卫星排列位置如图所示,则四颗卫星中,向心加速度最大的是( )
 有a、b、c、d四颗地球卫星,a还未发射,在地球赤道上某处放置,b在地球表面附近的近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星.各卫星排列位置如图所示,则四颗卫星中,向心加速度最大的是( )
有a、b、c、d四颗地球卫星,a还未发射,在地球赤道上某处放置,b在地球表面附近的近地轨道上正常运动,c是地球同步卫星,d是高空探测卫星.各卫星排列位置如图所示,则四颗卫星中,向心加速度最大的是( )| A. | a | B. | b | C. | c | D. | d |
2. 如图所示,由一段外皮绝缘的导线扭成两个半径为R和r圆形平面形成的闭合回路,R>r,导线单位长度的电阻为λ,导线截面半径远小于R和r.圆形区域内存在垂直平面向里、磁感应强度大小随时间按B=kt(k>0,为常数)的规律变化的磁场,下列说法正确的是( )
如图所示,由一段外皮绝缘的导线扭成两个半径为R和r圆形平面形成的闭合回路,R>r,导线单位长度的电阻为λ,导线截面半径远小于R和r.圆形区域内存在垂直平面向里、磁感应强度大小随时间按B=kt(k>0,为常数)的规律变化的磁场,下列说法正确的是( )
 如图所示,由一段外皮绝缘的导线扭成两个半径为R和r圆形平面形成的闭合回路,R>r,导线单位长度的电阻为λ,导线截面半径远小于R和r.圆形区域内存在垂直平面向里、磁感应强度大小随时间按B=kt(k>0,为常数)的规律变化的磁场,下列说法正确的是( )
如图所示,由一段外皮绝缘的导线扭成两个半径为R和r圆形平面形成的闭合回路,R>r,导线单位长度的电阻为λ,导线截面半径远小于R和r.圆形区域内存在垂直平面向里、磁感应强度大小随时间按B=kt(k>0,为常数)的规律变化的磁场,下列说法正确的是( )| A. | 小圆环中电流的方向为逆时针 | B. | 大圆环中电流的方向为逆时针 | ||
| C. | 回路中感应电流大小为$\frac{k({R}^{2}+{r}^{2})}{λ(R+r)}$ | D. | 回路中感应电流大小为$\frac{k(R-r)}{2λ}$ |
3. 如图所示,两个相同的细金属圆环带有等量异种电荷,相隔一定距离同轴平行固定放置,O1,、O2分别为两环圆心,一带正电的粒子从很远处沿水平轴线飞来并依次穿过两环,若粒子只受电场力作用,则在粒子运动过程中( )
如图所示,两个相同的细金属圆环带有等量异种电荷,相隔一定距离同轴平行固定放置,O1,、O2分别为两环圆心,一带正电的粒子从很远处沿水平轴线飞来并依次穿过两环,若粒子只受电场力作用,则在粒子运动过程中( )
 如图所示,两个相同的细金属圆环带有等量异种电荷,相隔一定距离同轴平行固定放置,O1,、O2分别为两环圆心,一带正电的粒子从很远处沿水平轴线飞来并依次穿过两环,若粒子只受电场力作用,则在粒子运动过程中( )
如图所示,两个相同的细金属圆环带有等量异种电荷,相隔一定距离同轴平行固定放置,O1,、O2分别为两环圆心,一带正电的粒子从很远处沿水平轴线飞来并依次穿过两环,若粒子只受电场力作用,则在粒子运动过程中( )| A. | 在经过O1点时粒子的速度最小 | |
| B. | 从O1到O2的过程中,粒子电势能一直增大 | |
| C. | 在轴线上O1点右侧一定存在一点,粒子在该点动能最小 | |
| D. | 轴线上O1点右侧、O2点左侧都存在合场强为零的点,且它们关于O1、O2连线中点对称 |

