题目内容
19.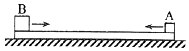 如图,两个滑块A和B的质量分别为mA=1kg和mB=5kg,放在静止与水平地面上的木板的两端,两者与木板间的动摩擦因数均为μ1=0.5;木板的质量为m=4kg,与地面间的动摩擦因数为μ2=0.1.某时刻A、B两滑块开始相向滑动,初速度大小均为v0=3m/s.A、B相遇时,A与木板恰好相对静止.设最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10m/s2.求
如图,两个滑块A和B的质量分别为mA=1kg和mB=5kg,放在静止与水平地面上的木板的两端,两者与木板间的动摩擦因数均为μ1=0.5;木板的质量为m=4kg,与地面间的动摩擦因数为μ2=0.1.某时刻A、B两滑块开始相向滑动,初速度大小均为v0=3m/s.A、B相遇时,A与木板恰好相对静止.设最大静摩擦力等于滑动摩擦力,取重力加速度大小g=10m/s2.求(1)B与木板相对静止时,木板的速度;
(2)A、B开始运动时,两者之间的距离.
分析 (1)刚开始运动时,根据牛顿第二定律分别求出A、B和木板的加速度大小,结合速度时间公式先求出B与木板共速时的速度以及运动的时间,然后B与木板保持相对静止,根据牛顿第二定律求出B与木板整体的加速度,结合速度时间公式求出三者速度相等经历的时间以及此时的速度.
(2)根据位移公式分别求出B与木板共速时木板和B的位移,从而得出两者的相对位移,得出此时A的位移以及A相对木板的位移大小,再结合位移公式分别求出三者速度相等时,A的位移以及木板的位移,得出A再次相对木板的位移,从而得出A、B开始运动时,两者之间的距离.
解答 解:(1)对A受力分析,根据牛顿第二定律得:μ1mAg=mAaA
代入数据解得:${a}_{A}=5m/{s}^{2}$,方向向右,
对B分析,根据牛顿第二定律得:μ1mBg=mBaB
代入数据解得:${a}_{B}=5m/{s}^{2}$,方向向左.
对木板分析,根据牛顿第二定律得:μ1mBg-μ1mAg-μ2(m+mA+mB)g=ma1
代入数据解得:${a}_{1}=2.5m/{s}^{2}$,方向向右.
当木板与B共速时,有:v=v0-aBt1=a1t1,
代入数据解得:t1=0.4s,v=1m/s,
(2)此时B相对木板静止,突变为静摩擦力,A受力不变加速度仍为5m/s2 ,方向向右,
对B与木板受力分析,有:μ1mAg+μ2(m+mA+mB)g=(m+mB)a2
代入数据解得:${a}_{2}=\frac{5}{3}m/{s}^{2}$,方向向左,
当木板与A共速时有:v′=v-a2t2=-v+aAt2:
代入数据解得:t2=0.3s,v′=0.5m/s.
当t1=0.4s,${x}_{B}=\frac{{v}_{0}+v}{2}{t}_{1}=\frac{3+1}{2}×0.4m=0.8m$,${x}_{木}=\frac{0+v}{2}{t}_{1}=\frac{0+1}{2}×0.4m=0.2m$
LB板=xB-x木=0.8-0.2m=0.6m,
对A,向左,${x}_{A}=\frac{{v}_{0}+v}{2}{t}_{1}=\frac{3+1}{2}×0.4m=0.8m$,
LA1板=xA+x木=0.8+0.2m=1m,
当t2=0.3s,对A,向左,${x}_{A1}=\frac{v-v′}{2}{t}_{2}=\frac{1-0.5}{2}×0.3m=\frac{3}{40}m$,
对木板,向右,${x}_{木1}=\frac{v+v′}{2}{t}_{2}=\frac{1+0.5}{2}×0.3m=\frac{9}{40}m$,
${L}_{A2板}={x}_{A1}+{x}_{木1}=\frac{3}{40}+\frac{9}{40}m=0.3m$,
可知AB相距L=LB板+LA1板+LA2板=0.6+1+0.3m=1.9m.
答:(1)B与木板相对静止时,木板的速度为1m/s;
(2)A、B开始运动时,两者之间的距离为1.9m.
点评 本题考查了牛顿第二定律和运动学公式的综合运用,关键理清整个过程中A、B和木板在整个过程中的运动规律,结合运动学公式和牛顿第二定律进行求解.

| A. | 角速度之比为ωⅠ:ωⅡ=2:1 | B. | 线速度之比为vⅠ:vⅡ=2:1 | ||
| C. | 向心加速度之比为aⅠ:aⅡ=2:1 | D. | 向心加速度之比为aⅠ:aⅡ=4:1 |
 如图所示,虚线EF左侧区域Ⅰ内有垂直纸面向里的匀强磁场,磁感应强度大小为B,右侧区域Ⅱ内有垂直于纸面向外的匀强磁场,磁感应强度大小为2B.边长为L、粗细均匀的正方形金属线框在区域Ⅰ内,线框平面与磁场垂直,cd边与虚线平行,线框的电阻为R,现使线框由图示位置以速度v向右匀速运动,则在线框通过EF的过程中( )
如图所示,虚线EF左侧区域Ⅰ内有垂直纸面向里的匀强磁场,磁感应强度大小为B,右侧区域Ⅱ内有垂直于纸面向外的匀强磁场,磁感应强度大小为2B.边长为L、粗细均匀的正方形金属线框在区域Ⅰ内,线框平面与磁场垂直,cd边与虚线平行,线框的电阻为R,现使线框由图示位置以速度v向右匀速运动,则在线框通过EF的过程中( )| A. | 通过线框截面的电量为$\frac{B{L}^{2}}{R}$ | |
| B. | 线框中电流的大小为$\frac{3BLv}{R}$ | |
| C. | 线框所受的安培力的大小为$\frac{6{B}^{2}{L}^{2}v}{R}$ | |
| D. | 线框中产生的焦耳热为$\frac{9{B}^{2}{L}^{3}v}{R}$ |
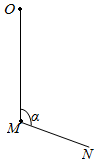 如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N.初始时,OM竖直且MN被拉直,OM与MN之间的夹角α(α>$\frac{π}{2}$).现将重物向右上方缓慢拉起,并保持夹角α不变,在OM由竖直被拉到水平的过程中( )
如图,柔软轻绳ON的一端O固定,其中间某点M拴一重物,用手拉住绳的另一端N.初始时,OM竖直且MN被拉直,OM与MN之间的夹角α(α>$\frac{π}{2}$).现将重物向右上方缓慢拉起,并保持夹角α不变,在OM由竖直被拉到水平的过程中( )| A. | MN上的张力逐渐增大 | B. | MN上的张力先增大后减小 | ||
| C. | OM上的张力逐渐增大 | D. | OM上的张力先增大后减小 |
 如图所示,两根平行金属导轨置于水平面内,导轨之间接有电阻R.金属棒ab与两导轨垂直并保持良好接触,整个装置放在匀强磁场中,磁场方向垂直于导轨平面向下.现使磁感应强度随时间均匀减小,ab始终保持静止,下列说法正确的是( )
如图所示,两根平行金属导轨置于水平面内,导轨之间接有电阻R.金属棒ab与两导轨垂直并保持良好接触,整个装置放在匀强磁场中,磁场方向垂直于导轨平面向下.现使磁感应强度随时间均匀减小,ab始终保持静止,下列说法正确的是( )| A. | ab中的感应电流方向由b到a | B. | ab中的感应电流逐渐减小 | ||
| C. | ab所受的安培力保持不变 | D. | ab所受的静摩擦力逐渐减小 |
 如图所示,将一光滑圆弧轨道固定竖直放置,其中A点为圆轨道的最低点,B点为圆水平直径与圆弧的交点.一个质量为m=1.256kg的物体静止于A点,现施加大小不变、方向始终和物体运动运动方向一致的外力F,使其沿圆周运动到达B点,随即撤去外力F,要使物体能在竖直圆轨道内维持圆周运动,π取3.14,g取10m/s2,外力F至少为( )
如图所示,将一光滑圆弧轨道固定竖直放置,其中A点为圆轨道的最低点,B点为圆水平直径与圆弧的交点.一个质量为m=1.256kg的物体静止于A点,现施加大小不变、方向始终和物体运动运动方向一致的外力F,使其沿圆周运动到达B点,随即撤去外力F,要使物体能在竖直圆轨道内维持圆周运动,π取3.14,g取10m/s2,外力F至少为( )| A. | 5N | B. | 10N | C. | 15N | D. | 20N |
| A. | 7.0m/s | B. | 7.7m/s | C. | 8.5m/s | D. | 10.0m/s |