题目内容
(2013·宁波模拟)1798年，英国物理学家卡文迪许测出万有引力常量G，因此卡文迪许被人们称为能称出地球质量的人。若已知万有引力常量G，地球表面处的重力加速度g，地球半径R，地球上一个昼夜的时间T1(地球自转周期)，一年的时间T2(地球公转的周期)，地球中心到月球中心的距离L1，地球中心到太阳中心的距离L2。你能计算出( )
A.地球的质量m地=
B.太阳的质量m太=
C.月球的质量m月=
D.可求月球、地球及太阳的密度
【解析】选A、B。由
解得地球的质量m地=，选项A正确；根据地球绕太阳运动的万有引力等于向心力可得出太阳的质量m太=，选项B正确；不能求出月球的质量和月球、太阳的密度，选项C、D错误。
练习册系列答案
相关题目
（2013?宁波模拟）如图所示电路中，电源电动势为E，线圈L的直流电阻不计，以下判断正确的是（ ）
（2013?宁波模拟）如图所示，固定在地面上的半圆轨道直径ab水平，质点P与半圆轨道的动摩擦因数处处一样，当质点P从a点正上方高H处自由下落，经过轨道后从b点冲出竖直上抛，上升的最大高度为H/2，空气阻力不计．当质点下落再经过轨道a点冲出时，能上升的最大高度h为（ ）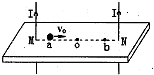
（2013?宁波模拟）如图所示，两根长直导线竖直插入光滑绝缘水平桌面上的M、N两小孔中，O为M、N连线中点，连线上a、b两点关于O点对称．导线均通有大小相等、方向向上的电流．已知长导线在周围产生的磁场的磁感应强度B=
（2013?宁波模拟）如图所示，速度不同的同种带电粒子（重力都不计）a、b沿半径．AO方向进入一圆形匀强磁场区域，a、b两粒子的运动轨迹分别为AB和AC，则下列说法中正确的是（ ）