题目内容
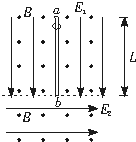 如图所示,水平虚线上方有场强为E1的匀强电场,方向竖直向下,虚线下方有场强为E2的匀强电场,方向水平向右;在虚线上、下方均有磁感应强度相同的匀强磁场,方向垂直纸面向外,ab是一长为L的竖直绝缘细杆,位于虚线上方,b端恰在虚线上,将一套在杆上的带电小环从a端由静止开始释放,小环先加速而后匀速到达b端,环与杆之间的动摩擦因数μ=0.3,小环的重力不计,当环脱离杆后在虚线下方沿原方向做匀速直线运动,求:
如图所示,水平虚线上方有场强为E1的匀强电场,方向竖直向下,虚线下方有场强为E2的匀强电场,方向水平向右;在虚线上、下方均有磁感应强度相同的匀强磁场,方向垂直纸面向外,ab是一长为L的竖直绝缘细杆,位于虚线上方,b端恰在虚线上,将一套在杆上的带电小环从a端由静止开始释放,小环先加速而后匀速到达b端,环与杆之间的动摩擦因数μ=0.3,小环的重力不计,当环脱离杆后在虚线下方沿原方向做匀速直线运动,求:(1)E1与E2 的比值;
(2)若撤去虚线下方的电场,小环进入虚线下方后的运动轨迹为半圆圆周半径为
| L | 3 |
分析:在上方磁场中当摩擦力与电场力的合力为零时匀速直线运动,在下方电场中电场力与洛伦兹力相等;
根据做圆周运动的半径求出匀速运动的速度大小,然后由动能定理求克服摩擦力做功Wf与电场力做功WE之比.
根据做圆周运动的半径求出匀速运动的速度大小,然后由动能定理求克服摩擦力做功Wf与电场力做功WE之比.
解答:解:(1)设小环在虚线上方达到的最大速度为v,在虚线上方运动时:qE1=μqvB
得:E1=μvB
在虚线下方运动时有:qE2=qvB
得:E2=Bv
故有:
=μ=0.3
(2)小环做圆周运动时有:qvB=m
得:r=
即:
=
得:v=
电场力做功:qE1L=q?μvB?L=
在虚线上方运动过程,根据动能定理:qEL-Wf=
mv2-0
得:Wf=
所以:
=
答:(1)E1与E2 的比值0.3.
(2)环从a到b的过程中克服摩擦力做功Wf与电场力做功WE之比为
.
得:E1=μvB
在虚线下方运动时有:qE2=qvB
得:E2=Bv
故有:
| E1 |
| E2 |
(2)小环做圆周运动时有:qvB=m
| v2 |
| r |
得:r=
| mv |
| qB |
即:
| mv |
| qB |
| L |
| 3 |
得:v=
| qBL |
| 3m |
电场力做功:qE1L=q?μvB?L=
| q2B2L2 |
| 10m |
在虚线上方运动过程,根据动能定理:qEL-Wf=
| 1 |
| 2 |
得:Wf=
| 2q2B2L2 |
| 45m |
所以:
| Wf |
| W电 |
| 4 |
| 9 |
答:(1)E1与E2 的比值0.3.
(2)环从a到b的过程中克服摩擦力做功Wf与电场力做功WE之比为
| 4 |
| 9 |
点评:带电粒子在电场、磁场的复合场中的运动,综合了静电场和力学的知识,分析方法和力学的分析方法基本相同.先分析受力情况再分析运动状态和运动过程(平衡、加速、减速,直线或曲线),然后选用恰当的规律解题.解决这类问题的基本方法有两种,第一种利用力和运动的观点,选用牛顿第二定律和运动学公式求解;第二种利用能量转化的观点,选用动能定理和功能关系求解.在解答有变力做功时,常用功能关系来解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
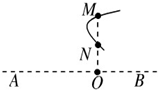 如图所示,水平虚线上有两个等量异种点电荷A、B,M、N、O是AB的垂线上两点,且AO>OB,2ON=OM,一个带正电的试探电荷在空间中运动的轨迹如图中实线所示,设M、N两点的场强大小分别EM、EN,电势分别为φM、φN,则下列判断错误的是( )
如图所示,水平虚线上有两个等量异种点电荷A、B,M、N、O是AB的垂线上两点,且AO>OB,2ON=OM,一个带正电的试探电荷在空间中运动的轨迹如图中实线所示,设M、N两点的场强大小分别EM、EN,电势分别为φM、φN,则下列判断错误的是( )| A、A点电荷一定带正电 | B、试探电荷在M处的电势能小于N处的电势能 | C、Em一定小于EN,φM可能大于φN | D、UMN=UNO |
 如图所示,水平虚线上有两个等量异种点电荷A、B,M、N是AB的垂线上两点,且AO>OB,2ON=OM.虚线的曲线表示空间中部分等势线的分布.一个带正电的试探电荷在空间中运动的轨迹如图中实线所示,设M、N两点的场强大小分别EM、EN,电势分别为φM、φN,则下列判断正确的是( )
如图所示,水平虚线上有两个等量异种点电荷A、B,M、N是AB的垂线上两点,且AO>OB,2ON=OM.虚线的曲线表示空间中部分等势线的分布.一个带正电的试探电荷在空间中运动的轨迹如图中实线所示,设M、N两点的场强大小分别EM、EN,电势分别为φM、φN,则下列判断正确的是( )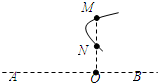 如图所示,水平虚线上有两个等量异种点电荷A、B,M、N、O是AB的垂线上两点,且AO>OB,2ON=OM.一个带正电的试探电荷在空间中运动的轨迹如图中实线所示,设M、N两点的场强大小分别EM、EN,电势分别为φM、φN,则下列判断正确的是( )
如图所示,水平虚线上有两个等量异种点电荷A、B,M、N、O是AB的垂线上两点,且AO>OB,2ON=OM.一个带正电的试探电荷在空间中运动的轨迹如图中实线所示,设M、N两点的场强大小分别EM、EN,电势分别为φM、φN,则下列判断正确的是( )
 ,则下列判断错误的是( )
,则下列判断错误的是( )
 可能大于
可能大于