题目内容
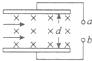
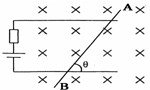
如图,与水平面成45°角的平面MN将空间分成Ⅰ和Ⅱ两个区域.一质量为m、电荷量为q(q>0)的粒子以速度v0从平面MN上的P0点水平右射入I区.粒子在Ⅰ区运动时,只受到大小不变、方向竖直向下的电场作用,电场强度大小为E;在Ⅱ区运动时,只受到匀强磁场的作用,磁感应强度大小为B,方向垂直于纸面向里.求粒子首次从Ⅱ区离开时到出发点P0的距离.粒子的重力可以忽略.


正粒子垂直电场进入做类平抛运动,初末位置在45°角的平面MN上,说明位移方向角是45°,
根据分解公式得x=v0t①y=
at2②a=
③tan45°=
④S=
x⑤v=
⑥
速度与水平方向的夹角θ:tanθ=2tan45°=2sinθ=
cosθ=
⑦
连立①②③④⑤⑥化简得v=
v0⑧S=2
进入磁场时与边界MN的夹角为θ-45°做匀速圆周运动,
根据牛顿第二定律得m
=Bqv⑨
作出原轨迹,则弦长和半径满足关系sin(θ-45°)=
⑩
连立⑨⑩得L=
所以粒子首次从II区离开时到出发点P0的距离为d=s+L=
(
+
)
根据分解公式得x=v0t①y=
| 1 |
| 2 |
| Eq |
| m |
| y |
| x |
| 2 |
|
速度与水平方向的夹角θ:tanθ=2tan45°=2sinθ=
| 2 | ||
|
| 1 | ||
|
连立①②③④⑤⑥化简得v=
| 5 |
| 2 |
m
| ||
| Eq |
进入磁场时与边界MN的夹角为θ-45°做匀速圆周运动,
根据牛顿第二定律得m
| v2 |
| R |
作出原轨迹,则弦长和半径满足关系sin(θ-45°)=
| L |
| 2R |
连立⑨⑩得L=
| 2 |
| mv0 |
| Bq |
所以粒子首次从II区离开时到出发点P0的距离为d=s+L=
| ||
| q |
| 2v0 |
| E |
| 1 |
| B |

练习册系列答案
相关题目