题目内容
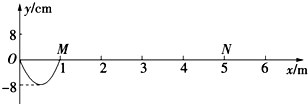
20. 如图所示,在y>0的空间中和y<0的空间内同时存在着大小相等,方向相反的匀强电场,上、下电场以x轴为分界线,在y轴左侧和图中竖直虚线MN右侧均无电场,但有方向垂直纸面向里和向外的匀强磁场,MN与y轴的距离为2d.一重力不计的负电荷从y轴上的P(0,d)点以沿x轴正方向的初速度v0开始运动,经过一段时间后,负电荷又以相同的速度回到P点,则下列说法正确的是( )
如图所示,在y>0的空间中和y<0的空间内同时存在着大小相等,方向相反的匀强电场,上、下电场以x轴为分界线,在y轴左侧和图中竖直虚线MN右侧均无电场,但有方向垂直纸面向里和向外的匀强磁场,MN与y轴的距离为2d.一重力不计的负电荷从y轴上的P(0,d)点以沿x轴正方向的初速度v0开始运动,经过一段时间后,负电荷又以相同的速度回到P点,则下列说法正确的是( )| A. | 电场与磁场的比值可能为v0 | |
| B. | 电场与磁场的比值可能为2v0 | |
| C. | 负电荷运动一个周期的时间为$\frac{2d}{{v}_{0}}$+$\frac{2πd}{{v}_{0}}$ | |
| D. | 负电荷运动一个周期的时间为$\frac{4d}{{v}_{0}}$+$\frac{2πd}{{v}_{0}}$ |
分析 粒子在电场中做类似平抛运动,在磁场中做匀速圆周运动,根据类似平抛运动的分运动公式和匀速圆周运动的半径公式、周期公式列式求解即可.
解答  解:A、B、粒子在电场中做类似平抛运动,根据类似平抛运动的分运动公式,有:
解:A、B、粒子在电场中做类似平抛运动,根据类似平抛运动的分运动公式,有:
d=v0t1
d=$\frac{1}{2}•\frac{qE}{m}•{t}_{1}^{2}$
粒子在磁场中做匀速圆周运动,有:
R=$\frac{m{v}_{0}}{qB}$
结合几何关系,有:
R=d
联立解得:
$\frac{E}{B}=2{v}_{0}$
故A错误,B正确;
C、D、类似平抛运动的时间:4t1=$\frac{4d}{{v}_{0}}$;
匀速圆周运动的轨迹是两个半圆,故时间:t2=$\frac{2πd}{{υ}_{0}}$;
带电粒子运动一个周期的时间为:t=$\frac{4d}{υ_0}+\frac{2πd}{υ_0}$,故C错误,D正确;
故选:BD.
点评 本题关键是明确粒子的运动规律,然后分类似平抛运动和匀速圆周运动考虑,不难.

练习册系列答案
相关题目
15. 一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.置于磁感应强度为B2的竖直向上的匀强磁场中,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,分析下述判断正确的有( )
一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.置于磁感应强度为B2的竖直向上的匀强磁场中,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,分析下述判断正确的有( )
 一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.置于磁感应强度为B2的竖直向上的匀强磁场中,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,分析下述判断正确的有( )
一个闭合回路由两部分组成,如图所示,右侧是电阻为r的圆形导线,置于竖直方向均匀变化的磁场B1中;左侧是光滑的倾角为θ的平行导轨,宽度为d,其电阻不计.置于磁感应强度为B2的竖直向上的匀强磁场中,一个质量为m、电阻为R的导体棒此时恰好能静止在导轨上,分析下述判断正确的有( )| A. | 圆形线圈中的磁场可以是向上均匀减弱 | |
| B. | 导体棒ab受到的安培力大小为mgsinθ | |
| C. | 回路中的感应电流为$\frac{mgtanθ}{{B}_{2}d}$ | |
| D. | 圆形导线中的电热功率为$\frac{{m}^{2}{g}^{2}rta{n}^{2}θ}{{{B}_{2}}^{2}{d}^{2}}$ |
5.应用物理知识分析生活中的常见现象,可以使物理学习更加深入有趣.例如平伸手掌托起物体,由静止开始竖直向上运动,直至将物体抛出.对此现象分析正确的是( )
| A. | 手托物体向上运动的过程中,物体始终处于超重状态 | |
| B. | 手托物体向上运动的过程中,当物体速度最大时,手和物体分离 | |
| C. | 在物体离开手的瞬间,手和物体的加速度大小相同 | |
| D. | 在物体离开手的瞬间,手的加速度大于重力加速度 |


 如图,光滑水平面上有一质量M=2kg的木块,初始时木块静止,现将一质量m=1kg的物体,轻轻靠在木块右侧上端,同时对木块施加水平向右的力F,已知水平面光滑,木块与物体之间的动摩擦因数为0.5,木块之间的最大静摩擦力等于滑动摩擦力,m离光滑水平面足够高,g=10m/s2,求:
如图,光滑水平面上有一质量M=2kg的木块,初始时木块静止,现将一质量m=1kg的物体,轻轻靠在木块右侧上端,同时对木块施加水平向右的力F,已知水平面光滑,木块与物体之间的动摩擦因数为0.5,木块之间的最大静摩擦力等于滑动摩擦力,m离光滑水平面足够高,g=10m/s2,求: