题目内容
竖直面内固定一个内部光滑的圆管,管的半径为r,管内有个直径和管的内径相差不多的小球(可看成质点),质量为m,在管内做圆周运动.小球到达最高点时,对管壁的压力大小为3mg,则小球在经过最高点时的速度大小为
A.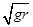 | B. | C. | D.2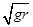 |
D
解析试题分析:小球到达最高点时,管壁对小球的压力由牛顿第三定律为3mg,方向竖直向下,则在最高点小球 受到的合力为:3mg+mg="4mg" ,由合力提供向心力得:4mg= ,解得:
,解得: ,D正确。
,D正确。
考点:本题考查向心力的来源。

练习册系列答案
相关题目
如图所示,某轻杆一端固定一质量为m的小球,以另一端O为圆心,使小球在竖直平面内做半径为R的圆周运动,以下说法中正确的是( )
| A.小球过最高点时,杆所受的弹力不可以为零 |
B.小球过最高点时,最小速度为 |
| C.小球过最低点时,杆对球的作用力不一定与小球所受重力方向相反 |
| D.小球过最高点时,杆对球的作用力可以与球所受重力方向相反,此时重力一定大于或等于杆对球的作用力 |
如图甲所示,轻杆一端固定在O点,另一端固定一小球,现让小球在竖直平面内做半径为R的圆周运动。小球运动到最高点时,杆与小球间弹力大小为F,小球在最高点的速度大小为v,其F—v2图象如乙图所示。则( )
A.小球的质量为 |
B.当地的重力加速度大小为 |
| C.v2 =c时,杆对小球的弹力方向向上 |
| D.v2=2b时,小球受到的弹力与重力大小相等 |
半径R=4cm的圆盘可绕圆心O水平转动,其边缘有一质量m=1kg的小物块(可视为质点),若物块随圆盘一起从静止开始加速转动,其向心加速度与时间满足a0=t2,物块与圆盘间的动摩擦因数为0.6,则:
| A.2s末圆盘的线速度大小为0.4m/s |
| B.2s末物块所受摩擦力大小为4N |
| C.物块绕完第一圈的时间约为1.88s |
| D.物块随圆盘一起运动的最大速度约为0.5m/s |
对于匀速圆周运动的物体,下列说法中错误的是( ).
| A.线速度不变 | B.角速度不变 | C.周期不变 | D.转速不变 |
图所示为一皮带传动装置,右轮的半径为r,A是它边缘上的一点,左侧是一轮轴,大轮的半径为4r,小轮的半径为2r;B点在小轮上,它到小轮中心的距离为r;C点和D点分别位于小轮和大轮的边缘上。若在传动过程中,皮带不打滑,则 ( )
| A.A点与B点的线速度大小相等 |
| B.A点与B点的角速度大小相等 |
| C.A点与C点的线速度大小不相等 |
| D.A点与D点的向心加速度大小相等 |


