题目内容

如图所示：在竖直面内固定着一个光滑
3
4
的圆弧轨道，O为圆心，OA水平，OB竖直，一小球从A点沿轨道射人，速度是v1，小球到达最高点B的速度是v2，则v1与v2比值可能是（　　）
分析：根据机械能守恒列式，可得v1与v2的关系，再根据小球到达最高点B的条件，列式，联立即可求得v1与v2比值．
解答：解：由机械能守恒得：
1
2
m
v
2
1
=mgR+
1
2
m
v
2
2
 ①
则得v1=
v
2
2
+2gR
  ②
所以
v1
v2
=
v
2
2
+2gR
v2
=
1+
2gR
v
2
2
 ③
要使小球能到达最高点，则必须满足的条件是：m
v
2
2
R
≥mg，v2≥
gR
  ④
由②③④得：1＜
v1
v2
≤
3

故CD正确，AB错误．
故选CD
点评：本题考查了机械能守恒和圆周运动临界条件，由机械能守恒和向心力知识得到速度比值的范围是解题关键．
练习册系列答案
相关题目
（2011?海淀区模拟）如图所示，在竖直面内有一以O点为圆心的圆，AB、CD分别为这个圆沿竖直和水平方向的直径，该圆处于静电场中．将带负电荷的小球从O点以相同的动能分别沿竖直平面向不同方向射出，小球会沿圆所在平面运动并经过圆周上不同的点．已知小球从O点分别到A、B两点的过程中电场力对它做的功相同，小球到达D点时的电势能大于它在圆周上其他各点时的电势能．若小球只受重力和电场力的作用，则下列说法中正确的是（　　）
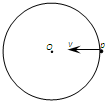精英家教网如图所示，在竖直面内有一个光滑弧形轨道，其末端水平，且与处于同一竖直面内光滑圆形轨道的最低端相切，并平滑连接．A、B两滑块（可视为质点）用轻细绳拴接在一起，在它们中间夹住一个被压缩的微小轻质弹簧．两滑块从弧形轨道上的某一高度由静止滑下，当两滑块刚滑入圆形轨道最低点时拴接两滑块的绳突然断开，弹簧迅速将两滑块弹开，其中前面的滑块A沿圆形轨道运动恰能通过轨道最高点．已知圆形轨道的半径R=0.50m，滑块A的质量mA=0.16kg，滑块B的质量mB=0.04kg，两滑块开始下滑时距圆形轨道底端的高度h=0.80m，重力加速度g取10m/s2，空气阻力可忽略不计．求：
（1）A、B两滑块一起运动到圆形轨道最低点时速度的大小；
（2）滑块A被弹簧弹开时的速度大小；
（3）弹簧在将两滑块弹开的过程中释放的弹性势能．
如图所示，在竖直面内有固定轨道ABCDE，其中BC是半径为R的四分之一圆弧轨道，AB（AB＞R）是竖直轨道，CE是足够长的水平轨道，CD＞R．AB与BC相切于B点，BC与CE相切于C点，轨道的AD段光滑，DE段粗糙且足够长．一根长为R的轻杆两端分别固定有质量均为m的相同小球P、Q（视为质点），将轻杆锁定在图示位置，此位置Q与B等高．现解除锁定释放轻杆，轻杆将沿轨道下滑，Q球经过D点后，沿轨道继续滑行了3R而停下．重力加速度为g．求：
（1）P球到达C点时的速度大小v1；
（2）两小球与DE段轨道间的动摩擦因数μ；
（3）Q球到达C点时的速度大小v2．
精英家教网如图所示，在竖直面内有一个圆轨道，圆心为O．P为轨道上与O等高的最右端位置，一小球以某一初速度从p点水平向左抛出，落在圆轨道上的某一点，忽略一切阻力和能量损耗，则下列说法正确的是（　　）
A、小球速度合适，球可能垂直撞在圆轨道上B、小球初速度合适，位移大小等于直径C、初速度越大，落到圆轨道上的时间越长D、小球初速度合适，落在O点正下方的圆周上时间最长

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网