题目内容
(10分)如图所示,小车的质量M=2kg,静止在光滑的水平面上,小车AB段水平,长L=1m,BC部分是光滑的1/4圆弧形轨道,半径R=0.4m,圆弧在C点的切线是竖直的。今有质量为m=1kg的金属滑块(宽度远小于小车的长度)以水平速度v0=5m/s冲上小车,金属滑块与小车AB段之间的动摩擦因数μ=0.3,试求:

(1)滑块上升的最大高度;
(2)小车获得的最大速度。
解析:
(1)设金属滑块上升的最大高度为H,上升到最大高度时金属滑块与小车具有共同速度![]() ,由动量守恒和能量守恒定律得
,由动量守恒和能量守恒定律得
mυ0=(m+M)![]() (2分)
(2分)
![]() (2分)
(2分)
解得H=0.53 m>R,说明金属滑块已经离开了小车。 (1分)
(2)由于C点切线是竖直方向,所以金属滑块离开小车时,在水平方向与小车具有相同速度,最后金属滑块又从C点落回小车.当金属滑块再次到达B点时,小车的速度达到最大.(1分)
设此时金属滑块的速度为υ1,小车的速度为υ2, 由动量守恒和能量守恒定律得
mυ0=mυ1+Mυ2 (1分)
![]() (2分)
(2分)
解得υ2=3 m/s(1分)(或υ2=![]() m/s舍去,这是金属滑块第一次到达B点时小车的速度)
m/s舍去,这是金属滑块第一次到达B点时小车的速度)

练习册系列答案
相关题目
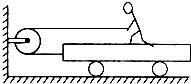 如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,又不计滑轮与绳的质量,则车对人的摩擦力不可能是( )
如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,又不计滑轮与绳的质量,则车对人的摩擦力不可能是( )| A、0 | ||
B、(
| ||
C、(
| ||
D、(
|
 如图所示,小车的质量为M,正在向右加速运动,一个质量为m的木块紧靠在车的前端相对于车保持静止,则下列说法正确的是( )
如图所示,小车的质量为M,正在向右加速运动,一个质量为m的木块紧靠在车的前端相对于车保持静止,则下列说法正确的是( ) 如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,不计滑轮与绳的质量,则车对人的摩擦力大小和方向不可能是( )
如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,不计滑轮与绳的质量,则车对人的摩擦力大小和方向不可能是( ) 如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,又不计滑轮与绳的质量,则车对人的摩擦力可能是( )
如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,又不计滑轮与绳的质量,则车对人的摩擦力可能是( ) 如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面光滑,不计滑轮与绳的质量,则车对人的摩擦力可能是( )
如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面光滑,不计滑轮与绳的质量,则车对人的摩擦力可能是( )