题目内容
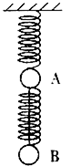 如图所示是两根轻弹簧与两个质量都为m的小球连接成的系统,上面一根弹簧的上端固定在天花板上,两小球之间还连接了一根不可伸长的细线.该系统静止,细线受到的拉力大小等于4mg.在剪断了两球之间的细线的瞬间,球A的加速度aA和球B的加速度aB分别是( )
如图所示是两根轻弹簧与两个质量都为m的小球连接成的系统,上面一根弹簧的上端固定在天花板上,两小球之间还连接了一根不可伸长的细线.该系统静止,细线受到的拉力大小等于4mg.在剪断了两球之间的细线的瞬间,球A的加速度aA和球B的加速度aB分别是( )分析:剪断细绳的瞬间,弹簧的弹力不变,根据牛顿第二定律求出物体a、b的瞬时加速度大小和方向.
解答:解:再剪断绳子之前,绳子的拉力为F=4mg
上边弹簧的拉力为F′=2mg,方向向上
下面弹簧的拉力为F″=4mg-mg=3mg,方向向下
间断瞬间,对A球受力分析可知
FA=F′+F″-mg=2mg+3mg-mg=4mg
FA=maA
aA=
=
=4g
方向向上
对B球分析
FB=F″+mg=4mg
FB=maB
aB=
=4g
方向向下
故选B
上边弹簧的拉力为F′=2mg,方向向上
下面弹簧的拉力为F″=4mg-mg=3mg,方向向下
间断瞬间,对A球受力分析可知
FA=F′+F″-mg=2mg+3mg-mg=4mg
FA=maA
aA=
| FA |
| m |
| 4mg |
| m |
方向向上
对B球分析
FB=F″+mg=4mg
FB=maB
aB=
| FB |
| m |
方向向下
故选B
点评:本题考查牛顿第二定律的瞬时问题,知道弹簧的弹力在瞬间不变,结合牛顿第二定律进行求解.

练习册系列答案
相关题目
如图所示是两根轻弹簧与两个质量都为m的小球连接成的系统,上面一根弹簧的上端固定在天花板上,两小球之间还连接了一根不可伸长的细线.该系统静止,细线受到的拉力大小等于4mg. 在剪断了两球之间的细线的瞬间,球A的加速度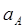 和球B的加速度
和球B的加速度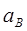 分别为( )
分别为( )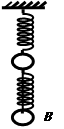
| A.2g,竖直向下;2g,竖直向下 |
| B.4g,竖直向上;4g,竖直向下 |
| C.2g,竖直向上;2g,竖直向下 |
| D.2g,竖直向下;4g,竖直向下 |
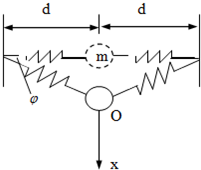 如图所示,两根轻弹簧的原长都是d,劲度系数都为k.由于质量为m的小球受重力作用,使系统处于实线所画的平衡位置,此时弹簧从水平位置下垂的倾角为φ.试证:此系统在竖直方向所作的小幅度振动为简谐振动,并求其固有的角频率.
如图所示,两根轻弹簧的原长都是d,劲度系数都为k.由于质量为m的小球受重力作用,使系统处于实线所画的平衡位置,此时弹簧从水平位置下垂的倾角为φ.试证:此系统在竖直方向所作的小幅度振动为简谐振动,并求其固有的角频率. 和球B的加速度
和球B的加速度 分别为( )
分别为( )
