题目内容
两质量相等的小球A和B，A球挂在一根长为L的细绳OA上，B球挂在橡皮绳OB上，将两球都拉到如图所示的水平位置上，两绳均拉直（此时橡皮绳为原长），然后无初速释放，当两球通过最低点C时，橡皮绳长与细绳长相等，小球A和B此时的速度分别为vA和vB，那么（ ）分析：重力做功公式WG=mgh．两球质量相等，根据高度比较重力做功的大小．根据能量守恒定律分析在最低点时两球速度的关系．
解答：解：两球质量相等，两球下降的高度都是L，根据重力做功公式WG=mgh得知，重力对两球做的功都是mgL，
根据能量守恒定律得：
对A球：mgL=
mvA2
对B球：mgL=
mvB2+EP，EP是橡皮绳的弹性势能
可见，在最低点A球速度vA大于B球的速度vB．故B正确，ACD错误．
故选：B．
根据能量守恒定律得：
对A球：mgL=
| 1 |
| 2 |
对B球：mgL=
| 1 |
| 2 |
可见，在最低点A球速度vA大于B球的速度vB．故B正确，ACD错误．
故选：B．
点评：利用功能关系解题时一定弄清功能的转化，不能漏掉某种能量，也不能凭空增加．
练习册系列答案
新思维假期作业寒假吉林大学出版社系列答案
相关题目
两质量相等的小球A和B，A球挂在一根长为L的细绳O’A上，B球挂在橡皮绳O′B上，现将两球都拉到如图的水平位置上，让两绳均拉直（此时橡皮绳为原长），然后无初速释放，当两球通过最低点O时，橡皮绳与细绳等长，小球A和B速度分别为vA和vB，那么（ ）
两质量相等的小球A和B，A球系在一根不可伸长的细绳的一端，B球系在一根原长小于细绳的橡皮绳一端，两绳的另一端都固定在O点，不计两绳质量．现将两球都拉到如图所示的水平位置上，让两绳均拉直（此时橡皮绳为原长），然后无初速释放，当两球通过O点正下方时，橡皮绳与细绳等长，小球A和B速度分别为vA和vB，那么（ ）
两质量相等的小球A和B，A球系在一根不可伸长的细绳的一端，B球系在一根原长小于细绳长度的橡皮筋一端，绳与橡皮筋的另一端都固定在O点，不计细绳和橡皮筋的质量．现将两球都拉到如图所示的位置上，让细绳和橡皮筋均水平拉直（此时橡皮筋为原长），然后无初速释放，当两球通过最低点时，橡皮筋与细绳等长，小球A和B速度大小分别为vA和vB．关于上述过程，下列说法中正确的是（ ）
有两质量相等的小球A和B，A挂在一根长为l的细绳上（绳子伸长不计），B挂在可伸长的较短的橡皮筋上，两球都拉到水平位置，如图所示，然后无初速释放，它们到达平衡位置时，橡皮筋的长度等于绳长l，则小球通过平衡位置时（ ）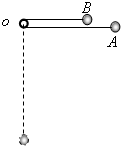
两质量相等的小球A和B，A球系在一根不可伸长的细绳一端，B球系在一根原长小于细绳的橡皮绳一端，两绳的另一端都固定在O点，不计两绳质量．现将两球都拉到如图所示的水平位置上，让两绳均拉直（此时橡皮绳为原长），然后无初速释放，当两球通过O点正下方时，橡皮绳与细绳恰好等长，那么（ ）