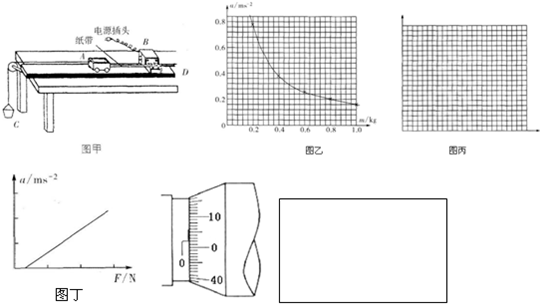
��Ŀ����
�ڡ�̽�����ٶ������������Ĺ�ϵ����ʵ���У�1��������������İ���˳���������뽫������˳������ĸ������д�ں�����
A������СͰ��ɳ�ӵ��������䣬��С��������룬������ٶȣ��ظ�����
B������С���������䣬�ı�СͰ��ɳ�ӵ�������������ٶȣ��ظ�����
C������ƽ���С����СͰ��ɳ�ӵ�����
D��ƽ��Ħ������ʹС������������ֱ���˶�
E������ɳͰ����ͨ����ʱ���ĵ�Դ���ſ�С������ֽ���ϴ���һϵ�еĵ�
F�����ݲ��������ݣ��ֱ�a-F��a-1/m��ͼ��
��2��������ֽ���ļ�¼��ͼ��ʾ����A����ÿ5����ȡһ�������㣬�������ڼ�������ʱ����Ϊ0.1s���������˶��ļ��ٶ�Ϊ

C��D��E��A��B��F��C��D��E��B��A��F��
C��D��E��A��B��F��C��D��E��B��A��F��
A������СͰ��ɳ�ӵ��������䣬��С��������룬������ٶȣ��ظ�����
B������С���������䣬�ı�СͰ��ɳ�ӵ�������������ٶȣ��ظ�����
C������ƽ���С����СͰ��ɳ�ӵ�����
D��ƽ��Ħ������ʹС������������ֱ���˶�
E������ɳͰ����ͨ����ʱ���ĵ�Դ���ſ�С������ֽ���ϴ���һϵ�еĵ�
F�����ݲ��������ݣ��ֱ�a-F��a-1/m��ͼ��
��2��������ֽ���ļ�¼��ͼ��ʾ����A����ÿ5����ȡһ�������㣬�������ڼ�������ʱ����Ϊ0.1s���������˶��ļ��ٶ�Ϊ
3.11
3.11
m/s2������3λ��Ч���֣�
��������1����ȷʵ��ԭ�����˽�ʵ��ľ������������ʵ�鲽��Ҫ�Ȱ�װ���ģ��ٽ���ʵ�����˳����У�
��2���������ȼ���ֱ�ߣ�������x=aT2������������˶��ļ��ٶȴ�С��
��2���������ȼ���ֱ�ߣ�������x=aT2������������˶��ļ��ٶȴ�С��
����⣺��1������ʵ�鲽��Ҫ�Ȱ�װ���ģ��ٽ���ʵ�����˳����У����ܵߵ���˳��Ҫ�����ڼ�Сʵ��������˳��Ϊ��C��D��E��A��B��F��C��D��E��B��A��F��
�ʴ�Ϊ��C��D��E��A��B��F��C��D��E��B��A��F��
��2���������ȼ���ֱ�ߣ�������x=aT2�ã�
s3-s1=2a1T2
s4-s2=2a2T2
a=
=
=3.11m/s2
�ʴ�Ϊ��3.11��
�ʴ�Ϊ��C��D��E��A��B��F��C��D��E��B��A��F��
��2���������ȼ���ֱ�ߣ�������x=aT2�ã�
s3-s1=2a1T2
s4-s2=2a2T2
a=
| a1+a2 |
| 2 |
| (s3+s4)-(s2+s1) |
| 4T2 |
�ʴ�Ϊ��3.11��
���������ʵ����������Ҫ���ո�ʵ��ԭ�����˽�ʵ��IJ�����������ݴ����Լ�ע���������Ӧ���ȱ���ֱ���˶��Ĺ��ɼ������۽�����⣮

��ϰ��ϵ�д�
�����Ŀ

 �ڡ�̽�����ٶ������Ĺ�ϵ��ʱ������С�����������䣬�ı�СͰ���������������ͬѧ����ʵ�����������˼��ٶ�a�����Fͼ����ͼ����ͼ�߲�ͨ������ԭ�㣬�Է���ͼ�߲�ͨ������ԭ���ԭ��
�ڡ�̽�����ٶ������Ĺ�ϵ��ʱ������С�����������䣬�ı�СͰ���������������ͬѧ����ʵ�����������˼��ٶ�a�����Fͼ����ͼ����ͼ�߲�ͨ������ԭ�㣬�Է���ͼ�߲�ͨ������ԭ���ԭ�� �ڡ�̽�����ٶ������������Ĺ�ϵ����ʵ���У���С������һ��ʱ������ʵ�����ݻ������ٶ�a��������F��ͼ����ͼ��ʾ��
�ڡ�̽�����ٶ������������Ĺ�ϵ����ʵ���У���С������һ��ʱ������ʵ�����ݻ������ٶ�a��������F��ͼ����ͼ��ʾ��