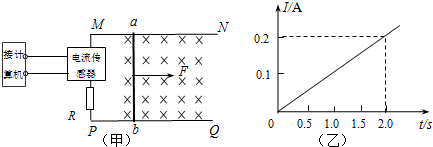题目内容
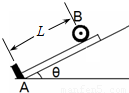
如图所示，金属杆静置于倾角θ=37°的斜面上，电动滚轮在斜面上方靠近金属杆上表面．在电动装置的控制下，逆时针匀速转动的电动滚轮能以不同的压力压在金属杆上表面．已知电动滚轮边缘的线速度为5m/s，它压紧在金属杆的上表面时，相对于地面的位置固定，其中心到斜面底端的距离L=4m，滚轮与金属杆间的动摩擦因数μ1=1.05，金属杆与斜面之间的动摩擦因数μ2=0.25，杆的质量为m=1×103kg，cos37°=0.8，sin37°=0.6，g取10m/s2．（1）要使金属杆能向上运动，滚轮对金属杆的压力FN必须大于多少？
（2）把金属杆离开斜面底端的最大距离定义为“发射距离x”．是否滚轮对金属杆的压力FN越大，发射距离x就越大？简要地说明理由．
（3）要使发射距离x=5m，求滚轮对金属杆的压力FN．设滚轮与金属杆接触的时间内压力大小不变．
【答案】分析：对木板受力分析，其向上运动的条件为向上的滑动摩擦力大于等于向下的摩擦力与重力分力之和；然后应用匀变速直线运动规律解题．
解答：解：（1）对金属杆受力分析如图所示，要使金属杆向上运动，
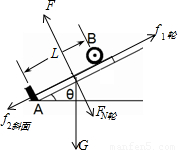
应有：μ1FN≥mgsinθ+μ2（FN+mgcosθ）
解得：FN≥10000N
所以要使金属杆能向上运动，滚轮对金属杆的压力FN必须大于10000N
（2）不是．
当压力增大时金属杆的加速度也增大，但当金属杆离开滚轮前的速度等于滚轮边缘的线速度，金属杆就做匀速运动，这时继续增大压力，金属杆离开滚轮的速度保持不变，发射距离也保持不变．
（3）金属杆离开滚轮后的加速度大小为：
a2=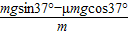
=8m/s2
金属杆离开滚轮上升的距离：x2=5m-4m=1m
金属杆离开滚轮的速度：v=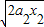
=4m/s
由于v＜5m/s，可见金属杆在与滚轮接触的时间内一直做匀加速运动，加速度为
a1=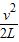
=2m/s2
由牛顿第二定律得：
μ1FN-mgsinθ+μ2（FN+mgcosθ）=ma1
代入数据得到FN=1.25×104N．
答：（1）要使金属杆能向上运动，滚轮对金属杆的压力FN必须大于10000N
（2）不是否滚轮对金属杆的压力FN越大，发射距离x就越大．
（3）要使发射距离x=5m，滚轮对金属杆的压力为1.25×104N．
点评：注意对应复杂的运动问题，往往是从受力分析入手，即物体的受力情况决定物体的运动的变化情况，所以一定要抓住这个突破口．
解答：解：（1）对金属杆受力分析如图所示，要使金属杆向上运动，
应有：μ1FN≥mgsinθ+μ2（FN+mgcosθ）
解得：FN≥10000N
所以要使金属杆能向上运动，滚轮对金属杆的压力FN必须大于10000N
（2）不是．
当压力增大时金属杆的加速度也增大，但当金属杆离开滚轮前的速度等于滚轮边缘的线速度，金属杆就做匀速运动，这时继续增大压力，金属杆离开滚轮的速度保持不变，发射距离也保持不变．
（3）金属杆离开滚轮后的加速度大小为：
a2=
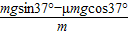=8m/s2金属杆离开滚轮上升的距离：x2=5m-4m=1m
金属杆离开滚轮的速度：v=
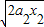=4m/s由于v＜5m/s，可见金属杆在与滚轮接触的时间内一直做匀加速运动，加速度为
a1=
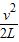=2m/s2由牛顿第二定律得：
μ1FN-mgsinθ+μ2（FN+mgcosθ）=ma1
代入数据得到FN=1.25×104N．
答：（1）要使金属杆能向上运动，滚轮对金属杆的压力FN必须大于10000N
（2）不是否滚轮对金属杆的压力FN越大，发射距离x就越大．
（3）要使发射距离x=5m，滚轮对金属杆的压力为1.25×104N．
点评：注意对应复杂的运动问题，往往是从受力分析入手，即物体的受力情况决定物体的运动的变化情况，所以一定要抓住这个突破口．
练习册系列答案
相关题目
