题目内容
如图所示，光滑的半球形物体固定在水平地面上，细线一端系住小球靠在半球面上A点，线的另一端在半球顶点正上方O1点，现将线的端点由点O1竖直缓慢上移至点O2，小球由点A缓慢移到点B，在此过程中，细线对小球的拉力T、半球对小球的支持力N的变化情况是（ ）分析：分析小球受力情况：重力G，细线的拉力T和半球面的支持力N，根据平行四边形定则作出N、T的合力F，根据正弦定理分析N、T的变化．
解答：解：以小球为研究对象，分析小球受力情况：重力G，细线的拉力T和半球面的支持力N，作出N、T的合力F，由平衡条件得知F=G．
A位置时支持力和拉力的情况如图中红线所示，
设支持力与拉力之间的夹角为θ，
根据正弦定理：
=
=
得：N=mg
；T=mg
B位置时支持力和拉力的情况如图中蓝线所示，
根据正弦定理：
=
=
得：N′=mg
；T′=mg
移到B点时α′＜α，β′＜β，θ′＞θ则sinα′＜sinα，sinβ′＜sinβ，sinθ′＞sinθ
故有：N′＜N，T′＜T；即T变小；N变小．
故选：C．
A位置时支持力和拉力的情况如图中红线所示，
设支持力与拉力之间的夹角为θ，
根据正弦定理：
| mg |
| sinθ |
| N |
| sinα |
| T |
| sinβ |
得：N=mg
| sinα |
| sinθ |
| sinβ |
| sinθ |
B位置时支持力和拉力的情况如图中蓝线所示，
根据正弦定理：
| mg |
| sinθ′ |
| N′ |
| sinα′ |
| T′ |
| sinβ′ |
得：N′=mg
| sinα′ |
| sinθ′ |
| sinβ′ |
| sinθ′ |
移到B点时α′＜α，β′＜β，θ′＞θ则sinα′＜sinα，sinβ′＜sinβ，sinθ′＞sinθ
故有：N′＜N，T′＜T；即T变小；N变小．
故选：C．
点评：本题是平衡问题中动态变化分析问题，N与T不垂直，故运用正弦定理，作为一种数学方法在物理中经常运用．
练习册系列答案
相关题目
如图所示，光滑的半球形物体固定在水平地面上，球心正上方有一光滑的小滑轮，轻绳的一端系一小球．靠放在半球上的A点，另一端绕过定滑轮后用力拉住，使小球静止．现缓慢地拉绳，在使小球沿球面由A到半球的顶点B的过程中，半球对小球的支持力N和绳对小球的拉力T的大小变化情况是（ ）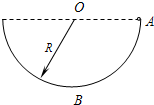
如图所示，光滑绝缘半球槽的半径为R，处在水平向右的匀强电场中，一质量为m的带电小球从槽的右端A处无初速沿轨道滑下，滑到最低位置B时，球对轨道的压力为2mg．求：
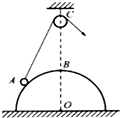如图所示，光滑的半球形物体固定在水平地面上，球心正上方有一光滑的小滑轮，轻绳的一端系一小球，靠在半球上的A点，另一端绕过定滑轮后用力拉住，使小球静止．现缓慢地拉绳，在使小球沿球面由A移动到半球的顶点B的过程中，半球对小球的支持力N和绳对小球的拉力T的变化情况是（ ）
)．