题目内容
 (2011?安徽模拟)如图所示,在平面直角坐标系XOY内,第I象限存在沿Y轴正方向的匀强电场,第IV象限内存在垂直于坐标平面向里的匀强磁场,磁感应强度大小设为B1(未知),第III象限内也存在垂直于坐标平面向里的匀强磁场B2(未知).一质量为m的电子(电量为e,不计重力),从Y轴正半轴上Y=h处的M点,以速度v0垂直于Y轴射入电场,经X轴上X=
(2011?安徽模拟)如图所示,在平面直角坐标系XOY内,第I象限存在沿Y轴正方向的匀强电场,第IV象限内存在垂直于坐标平面向里的匀强磁场,磁感应强度大小设为B1(未知),第III象限内也存在垂直于坐标平面向里的匀强磁场B2(未知).一质量为m的电子(电量为e,不计重力),从Y轴正半轴上Y=h处的M点,以速度v0垂直于Y轴射入电场,经X轴上X=2
| ||
| 3 |
(1)求匀强电场的场强大小E;
(2)求粒子经过Q点时速度大小和方向;
(3)求B1与B2之比为多少.
分析:(1)电子在电场中做类平抛运动,水平位移和竖直位移均已知,由牛顿第二定律和运动学公式,运用运动的分解法可求出场强大小E.
(2)由速度的合成法求出电子进入第IV象限磁场时的速度大小和方向,由几何知识确定粒子经过Q点时的方向.电子在磁场中速度的大小不变.
(3)由几何知识分别求出电子在两种磁场中运动的轨迹半径,由半径公式即可求出B1与B2之比.
(2)由速度的合成法求出电子进入第IV象限磁场时的速度大小和方向,由几何知识确定粒子经过Q点时的方向.电子在磁场中速度的大小不变.
(3)由几何知识分别求出电子在两种磁场中运动的轨迹半径,由半径公式即可求出B1与B2之比.
解答:解:(1)电子在电场中做类平抛运动,则
x=v0t=
h
h=
at2
又由牛顿第二定律得 a=
解得:E=
(2)画出电子在磁场中运动的轨迹图,
 vy=at=
vy=at=
v0
∴v=
=2v0
tanθ=
=
∴θ=60
∴∠OPO1=30° 又∵OQ=OP
由几何关系得∠OQO1=∠OPO1=30°
∴粒子到达Q点时速度方向与y轴正向成60°
(3)由几何关系得 r1cos30°+r1sin30°=op=
h
∴r1=(2-
)h
又r1=
=
进入B2后,
由几何关系得:2r2cos30°=OQ=OP=
h
∴r2=
h
又r2=
∴
=
=
答:
(1)匀强电场的场强大小E是
;
(2)粒子经过Q点时速度大小为2v0,方向与y轴正向成60°;
(3)B1与B2之比为
.
x=v0t=
| 2 |
| 3 |
| 3 |
h=
| 1 |
| 2 |
又由牛顿第二定律得 a=
| eE |
| m |
解得:E=
| 3mv02 |
| 2eh |
(2)画出电子在磁场中运动的轨迹图,
 vy=at=
vy=at=| 3 |
∴v=
|
tanθ=
| vy |
| v0 |
| 3 |
∴θ=60
∴∠OPO1=30° 又∵OQ=OP
由几何关系得∠OQO1=∠OPO1=30°
∴粒子到达Q点时速度方向与y轴正向成60°
(3)由几何关系得 r1cos30°+r1sin30°=op=
| 2 |
| 3 |
| 3 |
∴r1=(2-
| 2 |
| 3 |
| 3 |
又r1=
| mv |
| eB1 |
| 2mv0 |
| eB1 |
由几何关系得:2r2cos30°=OQ=OP=
| 2 |
| 3 |
| 3 |
∴r2=
| 2 |
| 3 |
又r2=
| 2mv0 |
| eB2 |
| B1 |
| B2 |
| r2 |
| r1 |
3+
| ||
| 6 |
答:
(1)匀强电场的场强大小E是
3m
| ||
| 2eh |
(2)粒子经过Q点时速度大小为2v0,方向与y轴正向成60°;
(3)B1与B2之比为
3+
| ||
| 6 |
点评:本题是带电粒子在电场和磁场中运动的问题,画出轨迹,运用几何知识求出电子的轨迹半径是解题的关键,同时要抓住几个过程之间的联系,比如速度关系、位移关系等

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
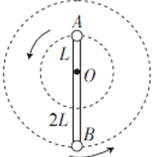 (2011?安徽模拟)如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,外界给予系统一定的能量后,杆和球在竖直面内转动.在转动的过程中,忽略空气的阻力.若球B运动到最高点时,球B对杆恰好无作用力,则下列说法正确的是( )
(2011?安徽模拟)如图所示,轻杆长为3L,在杆的A、B两端分别固定质量均为m的球A和球B,杆上距球A为L处的点O装在光滑的水平转动轴上,外界给予系统一定的能量后,杆和球在竖直面内转动.在转动的过程中,忽略空气的阻力.若球B运动到最高点时,球B对杆恰好无作用力,则下列说法正确的是( ) (2011?安徽模拟)如图所示为大型电子地磅电路图,电源电动势为E,内阻不计.不称物体时,滑片P到A端,滑动变阻器接入电路的有效电阻最大,电流较小;称重物时,在压力作用下使滑片P下滑,滑动变阻器有效电阻变小,电流变大,这样把电流对应的重量值刻在刻度盘上,就可以读出被称物体的重量值,若滑动变阻器上A、B间距离为L,最大阻值等于电阻阻值R0,已知两只弹簧的总弹力与形变量成正比,其比例系为k,所称重物的重量G与电流大小I的关系为( )
(2011?安徽模拟)如图所示为大型电子地磅电路图,电源电动势为E,内阻不计.不称物体时,滑片P到A端,滑动变阻器接入电路的有效电阻最大,电流较小;称重物时,在压力作用下使滑片P下滑,滑动变阻器有效电阻变小,电流变大,这样把电流对应的重量值刻在刻度盘上,就可以读出被称物体的重量值,若滑动变阻器上A、B间距离为L,最大阻值等于电阻阻值R0,已知两只弹簧的总弹力与形变量成正比,其比例系为k,所称重物的重量G与电流大小I的关系为( ) (2011?安徽模拟)如图所示,有一足够长斜面,倾角α=37°,一小物块质量为m,从斜面顶端A处由静止下滑,到B处后,受一与物体重力大小相等的水平向右恒力作用,开始减速,到C点减速到0(C点未画出).若AB=225m.物块与斜面间动摩擦因素μ=0.5,sin37°=0.6,cos37°=0.8,g=10m/s2.
(2011?安徽模拟)如图所示,有一足够长斜面,倾角α=37°,一小物块质量为m,从斜面顶端A处由静止下滑,到B处后,受一与物体重力大小相等的水平向右恒力作用,开始减速,到C点减速到0(C点未画出).若AB=225m.物块与斜面间动摩擦因素μ=0.5,sin37°=0.6,cos37°=0.8,g=10m/s2. (2011?安徽模拟)如图是某中学科技小组制作的利用太阳能驱动小车的装置.当太阳光照射到小车上方的光电板,光电板中产生的电流经电动机带动小车前进.若射到小车上方的光电板,光电板中产生的电流经电动机带动小车前进.若小车在平直的水泥路上从静止开始加速行驶,经过时间t前进距离s,速度达到最大值vm,设这一过程中电动机的功率恒为P,小车所受阻力恒为F,那么( )
(2011?安徽模拟)如图是某中学科技小组制作的利用太阳能驱动小车的装置.当太阳光照射到小车上方的光电板,光电板中产生的电流经电动机带动小车前进.若射到小车上方的光电板,光电板中产生的电流经电动机带动小车前进.若小车在平直的水泥路上从静止开始加速行驶,经过时间t前进距离s,速度达到最大值vm,设这一过程中电动机的功率恒为P,小车所受阻力恒为F,那么( )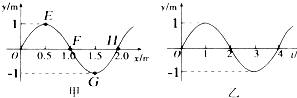 (2011?安徽模拟)一列沿着x轴正方向传播的横波,在t=2s时刻的波形如图甲所示,则图乙表示图甲中E、F、G、H四个质点中,哪一质点的振动图象( )
(2011?安徽模拟)一列沿着x轴正方向传播的横波,在t=2s时刻的波形如图甲所示,则图乙表示图甲中E、F、G、H四个质点中,哪一质点的振动图象( )