题目内容
如图所示，在直角坐标系x轴上方有与x轴成45°角的匀强电场，场强大小E=103V/m,在x轴下方有垂直纸面向外的匀强磁场，磁感应强度B=1T。现从y轴上距坐标原点L=1Ocm处由静止释放一比荷为
的带正电的微粒A,不计微粒的重力。求：
⑴微粒进入磁场后在磁场中运动的轨道半径；
⑵从释放微粒到微粒第一次从磁场返回电场所用时间；
⑶若在A第一次返回电场的同时，在电场中适当的位置由静止释放另一与A完全相同的带电微粒B,可使两微粒在进入磁场前相遇。求出所有满足条件的释放点的轨迹方程（不计两微粒之间的库仑力）。
解：⑴微粒在进入磁场前做匀加速运动，设微粒质量为m，带电量为q，进入磁场时速度为v，则：
…………………………………⑴（2分）
微粒进入磁场后做匀速圆周运动，设轨道半径为R，则：
……………………… ⑵（2分）
代入数值可解得：
m……………………… ⑶（2分）
⑵由此可作出微粒的运动轨迹如图所示。微粒在磁场中运动3/4圆周后从P点进入电场。设微粒从释放到进入电场之前所用时间为t，则：
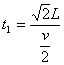………………………… ⑷（2分）
………………………… ⑸（2分）
而 
代入数值可得：
s………………………… ⑹（2分）
⑶微粒从P点进入磁场后做类平抛运动，设微粒再次进入磁场时距坐标原点为x，如图所示，则：
…………………………………………… ⑺（2分）
………………………………………………… ⑻（2分）
代入数值可解得
m ……………………………………… ⑼（1分）
由于微粒B与A完全相同，所以只需在微粒离开磁场时速度方向的直线上的PQ范围内任一点释放微粒B，可保证两者在进入磁场前相碰。即在直线
y=x +10 
………………………………………… ⑽（2分）
上式任意一点释放微粒B都能满足要求。
名师指导期末冲刺卷系列答案
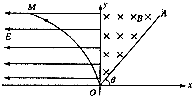如图所示，在直角坐标平面的第I象限内有一匀强磁场区域，磁感应强度为B，直线OA是磁场右侧的边界．在第Ⅱ象限区域，存在电场强度大小为E的水平向左的匀强电场，y轴是电场、磁场区域的分界线曲线，OM满足方程x=-ky2（k＞0）．有一带电荷量为q、质量为m的负粒子（重力不计）在曲线OM上某一点由静止释放，穿越y轴进入磁场中．
（2013?怀化二模）如图所示，在直角坐标xOy平面y轴左侧（含y轴）有一沿y轴负向的匀强电场，一质量为m，电量为q的带正电粒子从x轴上P处以速度ν0沿x轴正向进入电场，从y轴上Q点离开电场时速度变为2ν0，Q点坐标为（0，-d），在y轴右侧有一与坐标平面垂直的矩形匀强磁场区域（图中未画出，粒子过Q点继续运动一段距离后才进入磁场区域），磁场磁感应强度大小
如图所示，在直角坐标xOy平面y轴左侧（含y轴）有一沿y轴负向的匀强电场，一质量为m，电量为q的带正电粒子从x轴上P处以速度v0沿x轴正向进入电场，从y轴上Q点离开电场时速度方向与y轴负向夹角θ=30°，Q点坐标为（0，-d），在y轴右侧有一与坐标平面垂直的有界匀强磁场区域（图中未画出），磁场磁感应强度大小B=
如图所示，在直角坐标xoy的第一象限中分布着指向－y轴方向的匀强电场，在第四象限中分布着垂直纸面向里方向的匀强磁场，一个质量为m、带电＋q的粒子(不计重力)在A点(0，3)以初速V0＝120m/s平行x轴射入电场区域，然后从电场区域进入磁场，又从磁场进入电场，并且只通过x轴上的P点(6，0)和Q点(8，0)各一次，已知该粒子的荷质比为q/m＝108c/kg．
沿x轴正向进入电场，从y轴上Q点离开电场时速度方向与y轴负向夹角
，Q点坐标为（0，-d），在y轴右侧有一与坐标平面垂直的有界匀强磁场区域（图中未画出），磁场磁感应强度大小
，粒子能从坐标原点O沿x轴负向再进入电场．不计粒子重力，求：