题目内容
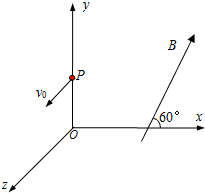 (2008?武汉二模)如图所示,在同时存在匀强电场和匀强磁场的空间中取正交坐标系Oxyz(x轴正方向水平向右,y轴正方向竖直向上).匀强磁场方向与Oxy平面平行,且与x轴的夹角为60°,重力加速度为g.一质量为m、电荷量为+q的带电质点沿平行于z轴正方向以速度v0做匀速直线运动.
(2008?武汉二模)如图所示,在同时存在匀强电场和匀强磁场的空间中取正交坐标系Oxyz(x轴正方向水平向右,y轴正方向竖直向上).匀强磁场方向与Oxy平面平行,且与x轴的夹角为60°,重力加速度为g.一质量为m、电荷量为+q的带电质点沿平行于z轴正方向以速度v0做匀速直线运动.(1)求电场强度的最小值Emin及对应的磁感应强度B;
(2)若电场强度为最小值Emin,当带电质点通过y轴上的点P(0,h,0)时,撤去匀强磁场,求带电质点落在Oxz平面内的位置.
分析:(1)若质点做直线运动,则一定是匀速直线运动,因为洛伦兹力受到速度的影响,所以三力处于平衡状态,根据力的合成与分解可列出洛伦兹力与重力的关系、电场力与重力的关系,从而确定电场强度的大小与方向;
(2)若撤去磁场,当带电质点P点射入时,只受到重力与电场力共同作用,质点做类平抛运动,根据平抛运动处理规律来确定质点的位置.
(2)若撤去磁场,当带电质点P点射入时,只受到重力与电场力共同作用,质点做类平抛运动,根据平抛运动处理规律来确定质点的位置.
解答:解:(1)如图答1所示,带电质点受到重力mg(大小及方向均已知)、洛伦兹力qv0B(方向已知)、电场力qE(大小及方向均未知)的作用做匀速直线运动.根据力三角形知识分析可知:当电场力方向与磁场方向相同时,场强有最小值Emin.根据物体的平衡规律有
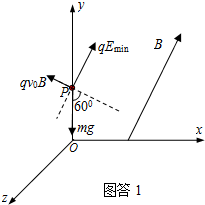
qEmin=mgsin60°①
qv0B=mgcos60°②
由①②得:Emin=
,B=
.
(2)如图答2所示,撤去磁场后,带电质点受到重力mg和电场力qEmin作用,其合力沿PM方向并与v0方向垂直,大小等于qv0B,故带电质点在与Oxz平面成30°角的平面内作类平抛运动.
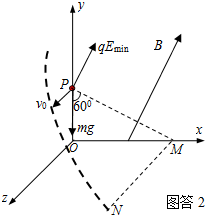
由牛顿第二定律 qv0B=ma ③
解得:a=0.5g.
设经时间t到达Oxz平面内的点N(x,y,z),由运动的分解可得
沿v0方向 z=v0t ④
沿PM方向 PM=
at2 ⑤
又 PM=
⑥
x=hcot30°⑦
联立③~⑦解得:x=
h,z=2v0
所以,带电质点落在N(
h,0,2υ0
)点(或带电质点落在Oxz平面内x=
h,z=2v0
的位置).
答:(1)电场强度的最小值Emin是
,对应的磁感应强度B是
;
(2)若电场强度为最小值Emin,当带电质点通过y轴上的点P(0,h,0)时,撤去匀强磁场,带电质点落在N(
h,0,2υ0
)点(或带电质点落在Oxz平面内x=
h,z=2v0
的位置).

qEmin=mgsin60°①
qv0B=mgcos60°②
由①②得:Emin=
| ||
| 2q |
| mg |
| 2qv0 |
(2)如图答2所示,撤去磁场后,带电质点受到重力mg和电场力qEmin作用,其合力沿PM方向并与v0方向垂直,大小等于qv0B,故带电质点在与Oxz平面成30°角的平面内作类平抛运动.

由牛顿第二定律 qv0B=ma ③
解得:a=0.5g.
设经时间t到达Oxz平面内的点N(x,y,z),由运动的分解可得
沿v0方向 z=v0t ④
沿PM方向 PM=
| 1 |
| 2 |
又 PM=
| h |
| sin30° |
x=hcot30°⑦
联立③~⑦解得:x=
| 3 |
|
所以,带电质点落在N(
| 3 |
|
| 3 |
|
答:(1)电场强度的最小值Emin是
| ||
| 2q |
| mg |
| 2qv0 |
(2)若电场强度为最小值Emin,当带电质点通过y轴上的点P(0,h,0)时,撤去匀强磁场,带电质点落在N(
| 3 |
|
| 3 |
|
点评:当质点做直线运动时,则有电场力、洛伦兹力与重力处于平衡状态,否则不可能做直线运动,原因是洛伦兹力受到速度的影响;当只受到电场力与重力时,若初速度与两力的合力相垂直,则做类平抛运动.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
 (2008?武汉二模)如图所示,均匀介质中两波源S1、S2分别位于x轴上x1=0、x2=14m处,质点P位于x轴上xp=4m处,t=0时刻两波源同时开始由平衡位置向y轴正方向振动,振动周期均为T=0.1s,传播速度均为v=40m/s,波源S1的振幅为A1=2cm,波源S2的振幅为A2=3cm,则从t=0至t=0.35s内质点P通过的路程为( )
(2008?武汉二模)如图所示,均匀介质中两波源S1、S2分别位于x轴上x1=0、x2=14m处,质点P位于x轴上xp=4m处,t=0时刻两波源同时开始由平衡位置向y轴正方向振动,振动周期均为T=0.1s,传播速度均为v=40m/s,波源S1的振幅为A1=2cm,波源S2的振幅为A2=3cm,则从t=0至t=0.35s内质点P通过的路程为( ) (2008?武汉二模)“绿色奥运”是2008年北京奥运会的三大理念之一,奥组委决定在各比赛场馆使用新型节能环保电动车,届时江汉大学的500名学生将担任司机,负责接送比赛选手和运输器材.在检测某款电动车性能的某次实验中,质量为8×102㎏的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F-
(2008?武汉二模)“绿色奥运”是2008年北京奥运会的三大理念之一,奥组委决定在各比赛场馆使用新型节能环保电动车,届时江汉大学的500名学生将担任司机,负责接送比赛选手和运输器材.在检测某款电动车性能的某次实验中,质量为8×102㎏的电动车由静止开始沿平直公路行驶,达到的最大速度为15m/s,利用传感器测得此过程中不同时刻电动车的牵引力F与对应的速度v,并描绘出F- (2008?武汉二模)如图所示,灯丝F发射的电子束经过电场加速后从阳极上的狭缝S穿出,通过两条平行狭缝S1、S2后,在荧光屏上形成明显的双缝干涉图样.已知一个电子从狭缝S穿出时动量为P,普朗克常量为h,则( )
(2008?武汉二模)如图所示,灯丝F发射的电子束经过电场加速后从阳极上的狭缝S穿出,通过两条平行狭缝S1、S2后,在荧光屏上形成明显的双缝干涉图样.已知一个电子从狭缝S穿出时动量为P,普朗克常量为h,则( ) (2008?武汉二模)如图所示,正方形线圈abcd位于纸面内,边长为L,匝数为N,过ab中点和cd中点的连线OO′恰好位于垂直纸面向里的匀强磁场的右边界上,磁感应强度为B,则穿过线圈的磁通量为( )
(2008?武汉二模)如图所示,正方形线圈abcd位于纸面内,边长为L,匝数为N,过ab中点和cd中点的连线OO′恰好位于垂直纸面向里的匀强磁场的右边界上,磁感应强度为B,则穿过线圈的磁通量为( )