题目内容

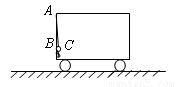
如图所示，一轻绳上端系在车的左上角的A点，另一轻绳一端系在车左端B点，B点在A点正下方，A、B距离为b，两绳另一端在C点相结并系一质量为m的小球，绳AC长度为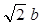，绳BC长度为b。两绳能够承受的最大拉力均为2mg。求：

(1)绳BC刚好被拉直时，车的加速度是多大?

(2)为不拉断轻绳，车向左运动的最大加速度是多大?

（要求画出受力图）

 

【答案】

（1）（7分）绳BC刚好被拉直时，小球受力如图所示

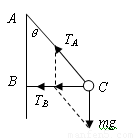
因为    AB=BC=b，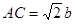

故 绳BC方向与AB垂直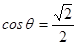，  θ=450  

由牛顿第二定律，得    mgtanθ=ma     

 可得   a=g    

（2）小车向左加速度增大，AB、BC绳方向不变，所以AC绳拉力不变，BC绳拉力变大，BC绳拉力最大时，小车向左加速度最大，小球受力如图分）

   由牛顿第二定律，得 Tm+ mgtanθ=mam   

因这时Tm=2mg       所以最大加速度为  am=3g

【解析】略

 

练习册系列答案
相关题目
（2007?江苏）如图所示，一轻绳吊着粗细均匀的棒，棒下端离地面高H，上端套着一个细环．棒和环的质量均为m，相互间最大静摩擦力等于滑动摩擦力kmg（k＞1）．断开轻绳，棒和环自由下落．假设棒足够长，与地面发生碰撞时，触地时间极短，无动能损失．棒在整个运动过程中始终保持竖直，空气阻力不计．求：
（1）棒第一次与地面碰撞弹起上升过程中，环的加速度；
（2）从断开轻绳到棒与地面第二次碰撞的瞬间，棒运动的路程S；
（3）从断开轻绳到棒和环都静止，摩擦力对环及棒做的总功W．
（2011?桂林一模）如图所示，一轻绳吊着粗细均匀的棒，棒下端离地面高H，上端套着一个细环，棒和环的质量均为m，相互间最大静摩擦力等于滑动摩擦力，大小为kmg（k＞1）．断开轻绳，棒和环自由下落，假设棒足够长，与地面发生碰撞时，触地时间极短，无动能损失，棒在整个运动过程中始终保持竖直，空气阻力不计，则（　　）
如图所示，一轻绳吊着粗细均匀的棒，棒下端离地面高H，上端套着一个细环．棒和环的质量均为m，相互间最大静摩擦力等于滑动摩擦力kmg（k＞1）．断开轻绳，棒和环自由下落．假设棒足够长，与地面发生碰撞时，触地时间极短，无动能损失．棒在整个运动过程中始终保持竖直，空气阻力不计．求：
（1）棒第一次与地面碰撞弹起上升过程中，环和棒的加速度．
（2）从断开轻绳到棒与地面第二次碰撞的瞬间，棒运动的路程s．
（3）与地面第二次碰撞前要使环不脱离棒，棒最少为多长？
（4）从断开轻绳到棒和环都静止，要使环不脱离棒，棒最少为多长？
精英家教网如图所示，一轻绳吊着粗细均匀的棒，棒下端离地面高H，上端套着一个细环．棒和环的质量均为m，相互间最大静摩擦力认为等于滑动摩擦力，大小为1.5mg．断开轻绳，棒和环开始竖直下落．假设棒足够长，与地面发生碰撞时，触地时间极短，无动能损失．棒在整个运动过程中始终保持竖直，空气阻力不计．则（　　）
A、棒第一次下落过程中，环做自由落体运动B、棒第一次与地面碰撞弹起上升过程中，棒做匀加速运动C、从断开轻绳到棒和环都静止的过程中，系统损失的机械能为2mgHD、从断开轻绳到棒和环都静止，环相对于地面通过的位移为5H

（07年江苏卷）（16分）如图所示，一轻绳吊着粗细均匀的棒，棒下端离地面高Ｈ，上端套着一个细环。

棒和环的质量均为m，相互间最大静摩擦力等于滑动摩擦力kmg(k>1)。断开轻绳，棒和环自由下落。假设棒足够长，与地面发生碰撞时，触地时间极短，无动能损失。棒在整个运动过程中始终保持竖直，空气阻力不计。求：

（1）棒第一次与地面碰撞弹起上升过程中，环的加速度。

（2）从断开轻绳到棒与地面第二次碰撞的瞬间，棒运动的路程S。

（3）从断开轻绳到棒和环都静止，摩擦力对环及棒做的总功W。

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网