题目内容
(17分)如图所示,轻质弹簧的一端固定在地面上,另一端与质量为M=1.5Kg的薄木板A相连,质量为m=0.5Kg的小球B放在木板A上,弹簧的劲度系数为k=2000N/m。现有一竖直向下、大小F=20N的力作用在B上且系统处于静止状态,在B球正上方处由一四分之一内壁光滑竖直圆弧轨道,圆弧半径R=0.4m,圆弧下端P点距离距离弹簧原长位置高度为h=0.6m。撤去外力F后,B竖直上升最终从P点切入原轨道,到达Q点的速度为vQ=4m/s。求:
(1)球B在Q点时对轨道的压力
(2)AB分离时的速度v
(3)撤去F瞬间弹簧的弹性是能Ep

【答案】
(1)15N(2)6m/s(3)36.4J
【解析】(1) 轨道对球压力N
N +mg=mvQ2/R (2分)
N =m vQ2/R –mg=15N (2分)
球对轨道压力N /= N = 15N (1分)
(2)AB在弹簧原长处分离后,B上升机械能守恒
mv2/2=mg(R+h)+ mvQ2/2 (2分)
v=6m/s (2分)
(3)撤去F到弹簧恢复原长AB分离上升H
kH=F+(m+M)g (2分)
H=0.02m (2分)
此过程机械能守恒
Ep=(m+M)gH+(m+M)v2/2 (2分)
代入数据得到 Ep=36.4J (2分)

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
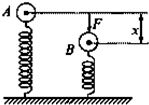 如图所示,轻质弹簧的劲度系数为k,小球重G,平衡时小球在A处,今用力F压小球至B处,使弹簧缩短x,则此时弹簧的弹力为( )
如图所示,轻质弹簧的劲度系数为k,小球重G,平衡时小球在A处,今用力F压小球至B处,使弹簧缩短x,则此时弹簧的弹力为( )| A、kx | B、kx+G | C、G-kx | D、以上都不对 |
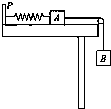 如图所示,轻质弹簧的一端固定在竖直板P上,另一端与质量为m1的物体A相连,物体A静止于光滑水平桌面上,A右边连接一细线绕过光滑的定滑轮悬挂一质量为m2的物体B(定滑轮的质量不计).开始时用手托住B,让细线恰好拉直,然后由静止释放B,直到B获得最大速度,下列有关此过程的分析正确的是( )
如图所示,轻质弹簧的一端固定在竖直板P上,另一端与质量为m1的物体A相连,物体A静止于光滑水平桌面上,A右边连接一细线绕过光滑的定滑轮悬挂一质量为m2的物体B(定滑轮的质量不计).开始时用手托住B,让细线恰好拉直,然后由静止释放B,直到B获得最大速度,下列有关此过程的分析正确的是( )| A、B物体机械能的减少量等于弹簧弹性势能与A物体动能的增加量之和 | B、A物体动能的增量等于细线拉力对A做的功 | C、B物体重力势能的减少量等于弹簧弹性势能的增加量 | D、A和B两物体的机械能之和一直保持不变 |
 如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A相连,A放在光滑水平面上,有一质量与A相同的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起将弹簧压缩,弹簧复原过程中某时刻B与A分开且沿原曲面上升.下列说法正确的是( )
如图所示,轻质弹簧的一端固定在墙上,另一端与质量为m的物体A相连,A放在光滑水平面上,有一质量与A相同的物体B,从高h处由静止开始沿光滑曲面滑下,与A相碰后一起将弹簧压缩,弹簧复原过程中某时刻B与A分开且沿原曲面上升.下列说法正确的是( ) 如图所示,轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小铁球,在电梯在竖直方向运行时,电梯内乘客发现弹簧的伸长量比电梯静止时的伸长量小了,这一现象表明( )
如图所示,轻质弹簧的上端固定在电梯的天花板上,弹簧下端悬挂一个小铁球,在电梯在竖直方向运行时,电梯内乘客发现弹簧的伸长量比电梯静止时的伸长量小了,这一现象表明( ) 如图所示,轻质弹簧的左端固定于竖直墙壁,右端悬空.一质量m=2.0kg的小球沿光滑水平地面以v0=4m/s的速度向左做匀速直线运动,碰撞轻质弹簧后原速离开弹簧.则:
如图所示,轻质弹簧的左端固定于竖直墙壁,右端悬空.一质量m=2.0kg的小球沿光滑水平地面以v0=4m/s的速度向左做匀速直线运动,碰撞轻质弹簧后原速离开弹簧.则: