题目内容
如图所示，两光滑平行导轨MN、PQ水平放置在竖直方向的匀强磁场中，两导轨间距为L，磁感应强度为B的匀强磁场与导轨所在平面垂直．质量为m的金属棒ab垂直导轨且可沿导轨自由移动，并与导轨良好接触．导轨左端M、P接一定值电阻R，金属棒ab的电阻为r，导轨电阻不计．现将金属棒ab沿导轨由静止向右拉使之平动，保持水平拉力的功率恒定，金属棒ab最终以速度3v作匀速运动．求：（1）金属棒匀速运动时，拉力的大小．
（2）在此过程中，当ab的速度为2v时的加速度为多大？
【答案】分析：（1）金属棒ab最终以速度3v作匀速运动，此时拉力与棒所受的安培力平衡，由F=BIL、I=
、E=BLv三个公式推导出安培力表达式，即可求得金属棒匀速运动时拉力的大小．
（2）拉力的功率恒定，求出匀速运动时拉力的功率，由P=Fv求得ab的速度为2v时的拉力，由牛顿第二定律求出加速度．
解答：解：（1）ab以3v匀速运动时，有F=F安
又F安=BIL
I=
E=BL?3v
得I=
由上面公式得：F=
（2）ab以3v匀速运动时拉力的功率为P=F?3v=
当ab的速度为2v时，有
拉力为 F′=
=
安培力为 F′安=BI′L=BL?
根据牛顿第二定律得
a=
=
答：
（1）金属棒匀速运动时，拉力的大小为
．
（2）在此过程中，当ab的速度为2v时的加速度为
．
点评：本题是收尾速度类型，与汽车恒定功率起动类似．此题推导安培力是解题的关键，
、E=BLv三个公式推导出安培力表达式，即可求得金属棒匀速运动时拉力的大小．（2）拉力的功率恒定，求出匀速运动时拉力的功率，由P=Fv求得ab的速度为2v时的拉力，由牛顿第二定律求出加速度．
解答：解：（1）ab以3v匀速运动时，有F=F安
又F安=BIL
I=
E=BL?3v
得I=
由上面公式得：F=
（2）ab以3v匀速运动时拉力的功率为P=F?3v=
当ab的速度为2v时，有
拉力为 F′=
=安培力为 F′安=BI′L=BL?
根据牛顿第二定律得
a=
=答：
（1）金属棒匀速运动时，拉力的大小为
．（2）在此过程中，当ab的速度为2v时的加速度为
．点评：本题是收尾速度类型，与汽车恒定功率起动类似．此题推导安培力是解题的关键，
练习册系列答案
相关题目
（2006?静安区模拟）如图所示，两光滑平行导轨MN、PQ水平放置在匀强磁场中，磁场与导轨所在平面垂直，金属棒ab可沿导轨自由移动，导轨左端M、P接一定值电阻，金属棒和导轨电阻均不计，现将金属棒沿导轨由静止向右拉，若保持拉力F恒定，经时间t1后速度为v，加速度为a1，最终以速度2v做匀速运动；若保持拉力的功率不变，经过时间t2后，速度为v，加速度为a2，最终也以2v做匀速运动，求a1和a2的比值？
（2012?昆山市模拟）如图所示，两光滑平行导电导轨水平放置于磁感应强度为B的匀强磁场中，磁场与导轨所在平面垂直．已知金属棒ab能沿导轨自由移动，且导轨一端跨接一个定值电阻R，金属棒与导轨电阻均不计．现将金属棒沿导轨以初速度v0开始向右拉动，若保持拉力恒定不变，经过时间t1后金属棒速度变为v，加速度为a1，最终以速度2v做匀速运动．若再使金属棒仍以初速度v0开始，保持拉力的功率不变，经过时间t2后金属棒速度变为v，加速度为a2，最终以速度2v做匀速运动．则（ ）
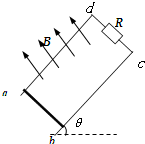如图所示，两光滑平行的金属导轨所在的平面与水平面成一角，导轨上端cd通过电阻R连接（不计电路中的其它电阻），匀强磁场垂直穿过导轨平面．若金属杆ab以沿平行于导轨平面大小为2| gh |
| A、上行过程中流过电阻R上的感应电流的方向是由c端流向d端 |
| B、上行时间小于下行时间 |
| C、上行过程中电阻R上产生的热量比下行时的大 |
| D、上行过程导体杆ab受到的磁场力的冲量的大小跟下行时的不相等 |
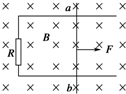如图所示，两光滑平行导轨水平放置在匀强磁场中，磁场垂直导轨所在平面，金属棒ab可沿导轨自由滑动，导轨一端跨接一个定值电阻R，导轨电阻不计．现将金属棒沿导轨由静止向右拉，若保持拉力F恒定，经过时间t1后速度为v，加速度为a1，最终以速度2v做匀速运动；若保持拉力的功率P恒定，棒由静止经时间t2后速度为v，加速度为a2，最终也以速度2v做匀速运动，则（ ）