Question

如图所示，用一个三角支架悬挂重物，已知AB杆所能承受的最大压力为2 000 N，AC绳所能承受的最大拉力为1 000 N，∠α＝30°，为不使支架断裂，求悬挂物的重力应满足的条件．

Answer 1

答案：
解析：

答案：Gm≤F2sin30°＝500 N． 　　思路解析：由下图可知： 　　F1＝　　F2＝ 　　即＝，因为AB、AC能承受的最大作用力之比为 　　当悬挂物重力增大时，对AC绳的拉力将先达到最大值，所以为不使三角架断裂，计算中应以AC绳中拉力达最大值为依据，即取F2＝F2m＝1 000 N，于是得悬挂物的重力应满足的条件为Gm≤F2sin30°＝500 N．

提示：

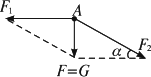
该题属于共点力平衡条件考查的常规题，采用的是分解法．悬绳A点受到竖直向下的拉力F＝G，这个拉力将压紧水平杆AB并拉引绳索AC，所以应把拉力F沿AB、CA两方向分解，设两分力为F1、F2，画出的平行四边形如图所示．在该类问题中，一定要清楚当物体的重力逐渐增大时，哪一个首先断裂．然后依据最先断裂的物体来求物体的最大重力．