题目内容
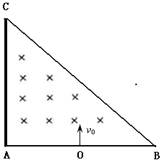 如图所示,等腰直角三角形ABC的区域内有一垂直于纸面向内的匀强磁场,磁感应强度为B,已知AB=2a,现有一束质量为m,带电量为q的正粒子在AB的中点O处沿着垂直与AB的方向以v0打入磁场,在AC边上放置一块足够大的荧光屏,当v0=
如图所示,等腰直角三角形ABC的区域内有一垂直于纸面向内的匀强磁场,磁感应强度为B,已知AB=2a,现有一束质量为m,带电量为q的正粒子在AB的中点O处沿着垂直与AB的方向以v0打入磁场,在AC边上放置一块足够大的荧光屏,当v0=| 3aqB | m |
(1)判断粒子能否打到荧光屏上.
(2)求粒子在磁场中运动的时间.
分析:(1)带电粒子在磁场中做匀速圆周运动,由洛仑兹力提供向心力,根据牛顿第二定律和v0=
,求出轨迹半径.
从0处打入磁场的粒子,当轨迹与BC相切时,由几何知识得出这种情况下轨迹的半径,与粒子的轨迹半径进行比较,判断粒子能否打到荧光屏上.
(2)画出粒子的轨迹,求出圆心角,根据时间与周期的关系求解时间.
| 3aqB |
| m |
从0处打入磁场的粒子,当轨迹与BC相切时,由几何知识得出这种情况下轨迹的半径,与粒子的轨迹半径进行比较,判断粒子能否打到荧光屏上.
(2)画出粒子的轨迹,求出圆心角,根据时间与周期的关系求解时间.
解答: 解:(1)带电粒子在磁场中做匀速圆周运动,由洛仑兹力提供向心力,有:qv0B=m
解:(1)带电粒子在磁场中做匀速圆周运动,由洛仑兹力提供向心力,有:qv0B=m
当:v0=
时,R=3a
从0处打入的粒子当轨迹与BC相切时,知该圆轨迹的半径R1(图中虚线所示)满足:R1+a=
R1
得 R1=(
+1)a<R=3a
所以粒子不能打到荧光屏上
(2)以v0打入的粒子轨迹如图(轨迹半径为图中实线所示),圆心为O′,圆心角为α,从BC边上出射点为D,过D作AB垂线,垂足为E,设DE=x,则有:
R+a=Rsinα+Rcosα
得:sin2α=
α=
arcsin
运动时间为t=
T=
?
=
=
答:
(1)粒子不能打到荧光屏上.
(2)粒子在磁场中运动的时间为
.
 解:(1)带电粒子在磁场中做匀速圆周运动,由洛仑兹力提供向心力,有:qv0B=m
解:(1)带电粒子在磁场中做匀速圆周运动,由洛仑兹力提供向心力,有:qv0B=m
| ||
| R |
当:v0=
| 3aqB |
| m |
从0处打入的粒子当轨迹与BC相切时,知该圆轨迹的半径R1(图中虚线所示)满足:R1+a=
| 2 |
得 R1=(
| 2 |
所以粒子不能打到荧光屏上
(2)以v0打入的粒子轨迹如图(轨迹半径为图中实线所示),圆心为O′,圆心角为α,从BC边上出射点为D,过D作AB垂线,垂足为E,设DE=x,则有:
R+a=Rsinα+Rcosα
得:sin2α=
| 7 |
| 9 |
α=
| 1 |
| 2 |
| 7 |
| 9 |
运动时间为t=
| α |
| 2π |
| α |
| 2π |
| 2πm |
| qB |
| αm |
| qB |
marcsin
| ||
| 2qB |
答:
(1)粒子不能打到荧光屏上.
(2)粒子在磁场中运动的时间为
marcsin
| ||
| 2qB |
点评:本题实质是有界磁场的问题,分析临界情况下粒子能否射出BC是关键.求带电粒子做匀速圆周运动的时间常常用到t=
T求时间,α是轨迹的圆心角.
| α |
| 2π |

练习册系列答案
相关题目
如图所示是等腰直角三棱柱,其中底面abcd为正方形,边长为L,它们按图示位置放置于竖直向下的匀强磁场中,磁感应强度为B,下面说法中正确的是( )
| A.通过abcd平面的磁通量大小为L2·B |
B.通过dcfe平面的磁通量大小为 L2·B L2·B |
| C.通过abfe平面的磁通量大小为零 |
| D.通过bcf平面的磁通量为零 |
 如图所示,等腰直角三角形ABC,O为斜边AC边的中点.在A、B、C三个顶点处分别放置三根通电长直导线,导线中的电流大小相等,方向均垂直纸面向里.则三根通电直导线在O点共同产生的磁场的方向为图中( )
如图所示,等腰直角三角形ABC,O为斜边AC边的中点.在A、B、C三个顶点处分别放置三根通电长直导线,导线中的电流大小相等,方向均垂直纸面向里.则三根通电直导线在O点共同产生的磁场的方向为图中( ) 如图所示是等腰直角三棱柱,其中底面abcd为正方形,边长为L,它们按图示位置放置于竖直向下的匀强磁场中,磁感应强度为B,下面说法中正确的是( )
如图所示是等腰直角三棱柱,其中底面abcd为正方形,边长为L,它们按图示位置放置于竖直向下的匀强磁场中,磁感应强度为B,下面说法中正确的是( )
 L2·B
L2·B 
