题目内容
水平面上两小球在同一直线上同向运动,后球追上前球发生正碰,试证明碰撞前后两小球的总动量守恒.
分析:根据牛顿第二定律和牛顿第三定律列式证明.
解答:证明:设前面小球是1球,后面为2球,
根据牛顿第二定律,碰撞过程中1、2两球的加速度分别是:
a1=
a2=
根据牛顿第三定律,F1、F2等大反向,即 F1=-F2
所以:m1a1=-m2a2
碰撞时两球间的作用时间极短,用△t表示,则有:
a1=
a2=
代入得:m1v1+m2v2=m1v′1+m2v′2
即得碰撞前后两小球的总动量守恒.
根据牛顿第二定律,碰撞过程中1、2两球的加速度分别是:
a1=
| F1 |
| m1 |
| F2 |
| m2 |
根据牛顿第三定律,F1、F2等大反向,即 F1=-F2
所以:m1a1=-m2a2
碰撞时两球间的作用时间极短,用△t表示,则有:
a1=
| v′1-v1 |
| △t |
a2=
| v′2-v2 |
| △t |
代入得:m1v1+m2v2=m1v′1+m2v′2
即得碰撞前后两小球的总动量守恒.
点评:解决该题关键要掌握牛顿第二定律和牛顿第三定律的应用.

练习册系列答案
相关题目
 (2009?南开区一模)如图所示,两杆所在平面与桌面垂直.杆上各穿一个质量为10g的小球,可沿杆无摩擦滑动,两球均带10-7C的正电荷,求:
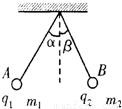
(2009?南开区一模)如图所示,两杆所在平面与桌面垂直.杆上各穿一个质量为10g的小球,可沿杆无摩擦滑动,两球均带10-7C的正电荷,求: 如图所示,两带电小球A和B各用细线悬挂于同一点,平衡时,两小球在同一水平面上,悬线与竖直方向的夹角分别为α和β,且α>β.关于两球的质量m1和m2及电量q1和q2,可以断定( )
如图所示,两带电小球A和B各用细线悬挂于同一点,平衡时,两小球在同一水平面上,悬线与竖直方向的夹角分别为α和β,且α>β.关于两球的质量m1和m2及电量q1和q2,可以断定( )