Question

（2009?盐城模拟）如图所示，传送带的倾角为θ=53°，AB的长度为37.5m．传送带以11m/s的速度运动．在传送带的上端A，无初速度地放一个质量为0.5kg的物体，它与传送带之间的动摩擦因数为0.5．则物体从A运动到B所用的时间可能为（已知sin53°=0.8，cos53°=0.6，g取10m/s²）（　　）

• A．3.0s
• B．2s
• C．

  15

  s
• D．4s

Answer 1

分析：本题传送带转动方向不定，要分两种情况进行讨论，若传送带逆时针转动，当物块速度小于传送带时，滑动摩擦力方向向下，根据牛顿第二定律求出加速度，根据运动学基本公式求出速度到达与传送带速度相等的时间和位移，比较这个位移和AB的长度，若AB长度长，则此后滑动摩擦力方向向上，根据牛顿第二定律求出加速度，根据运动学基本公式求解时间，两者之和即为总时间；
若传送带顺时针转动，则A一直做匀加速运动到B点，根据位移时间公式求解时间．

解答：解：若传送带逆时针转动，在物体开始运动的开始阶段受力如图（a）所示，由牛顿第二定律得：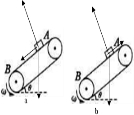
mgsinθ+μmgcosθ=ma
解得加速度：a=gsinθ+μgcosθ=11m/s²．
物体加速至与传送带速度相等时需要的时间为：t₁=

v

a

=

11

11

=1s
发生的位移为：s₁=

1

2

at12=

1

2

×11×1=5.5m＜37.5m．
可知物体加速到11m/s时仍未到达B点．　　　　 
第二阶段的受力分析如图（b）所示，应用牛顿第二定律，有：
mgsinθ-μmgcosθ=ma₂，所以此阶段的加速度为：a₂=5m/s²
设第二阶段物体滑动到B端的时间为t₂，则：L_AB-s₁=vt₂+

1

2

a₂t₂²
解得：t₂=2s?
故物体经历的总时间：t=t₁+t₂=3s
若传送带顺时针转动，则A一直做匀加速运动到B点，则有：
L=

1

2

a₂t²
解得；t=

15

s
故选AC

点评：解决本题的关键理清物体的运动，分两种情况讨论，物体可能经历了两个匀加速直线运动，加速度大小不等，也可能一直做匀加速运动，结合牛顿第二定律和运动学公式进行求解．