题目内容
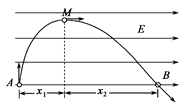
（17分）如图所示，光滑固定轨道的两端都是半径为R的四分之一圆弧，在轨道水平面上有两个质量均为m的小球B、C，B、C用一长度锁定不变的轻小弹簧栓接，弹性势能
．一质量也为m的小球A从左侧的最高点自由滑下，A滑到水平面与B碰后立即粘在一起结合成D就不再分离（碰撞时间极短）．当D、C一起刚要滑到右侧最低点时，弹簧锁定解除且立即将C弹出并与弹簧分离．求
（1）弹簧锁定解除前瞬间，D、C速度大小
（2）弹簧锁定解除后，C第一次滑上轨道右侧圆弧部分的轨迹所对的圆心角
（3）弹簧锁定解除后，若C、D（含弹簧）每次碰撞均在水平面；求第N次碰撞结束时，C、D的速度
(1)
（2）
（3）当N为奇数时：
；当N为偶数时:
解析试题分析: (1)小球A下滑由动能定理：
①
A与B碰撞满足动量守恒： 
②
由①②解得： ③
(2)由动量守恒：
④
机械能守恒：
⑤
由③④⑤解得： 
或
⑥
⑦
由⑥⑦解得
（3）以左为正方向
第一次：
⑧
⑨
由⑧⑨得
或
⑩
第二次：
?
?
由⑩??解得：
或
综上，当N为奇数时： ；当N为偶数时:
考点：本题考查了动能定理、机械能守恒定律、动量守恒定律。
练习册系列答案
相关题目
的电场加速后，从水平放置的一对平行金属板正中间水平射入偏转电场中，若金属极板长L＝0.05m，两极板间距d＝0.02m ，求：两板间至少要加多大的电压 
才能使电子不飞出电场
