题目内容
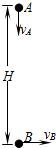 (2011?天门模拟)如图所示,小洁将小球甲从空中A点以υA=3m/s的速度竖直向下抛出,同时小明将另一小球乙从A点正下方H=10m的B点以υB=4m/s的速度水平抛出,不计空气阻力,B点离地面足够高,求两球在空中的最短距离.
(2011?天门模拟)如图所示,小洁将小球甲从空中A点以υA=3m/s的速度竖直向下抛出,同时小明将另一小球乙从A点正下方H=10m的B点以υB=4m/s的速度水平抛出,不计空气阻力,B点离地面足够高,求两球在空中的最短距离.分析:A做竖直下抛运动,B做平抛运动,设经过时间t位移最短,根据运动学基本规律求出两球之间的距离的表达式,结合数学知识即可求解.
解答:解:经过时间t,A做竖直下抛运动的位移为:y甲=υAt+
gt2
B在竖直方向做自由落体运动的位移为:y乙=
gt2
两球在竖直方向的距离为:y=H+y乙-y甲
B在水平方向的位移,即两球在水平方向的距离为:x=υBt
所以,两球之间的距离为:s=
联立以上各式解得:s=
当t=1.2s时,两球之间最短距离为smin=8m
答:两球在空中的最短距离为8m.
| 1 |
| 2 |
B在竖直方向做自由落体运动的位移为:y乙=
| 1 |
| 2 |
两球在竖直方向的距离为:y=H+y乙-y甲
B在水平方向的位移,即两球在水平方向的距离为:x=υBt
所以,两球之间的距离为:s=
| x2+y2 |
联立以上各式解得:s=
| (10-3t)2+(4t)2 |
当t=1.2s时,两球之间最短距离为smin=8m
答:两球在空中的最短距离为8m.
点评:本题主要考查了竖直下抛运动和做平抛运动的基本规律,求某个量的极值时可以先把这个量的表达式求出来,再结合数学知识求解,难度适中.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目

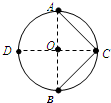 (2011?天门模拟)如图所示,AB、CD为一圆的两条直径,且相互垂直,O点为圆心.空间存在一未知静电场,场强方向与圆周所在平面平行.现有一电子,在电场力作用下(重力不计),先从A点运动到C点,动能减少了W;又从C点运动到B点,动能增加了W,那么关于此空间存在的静电场可能是( )
(2011?天门模拟)如图所示,AB、CD为一圆的两条直径,且相互垂直,O点为圆心.空间存在一未知静电场,场强方向与圆周所在平面平行.现有一电子,在电场力作用下(重力不计),先从A点运动到C点,动能减少了W;又从C点运动到B点,动能增加了W,那么关于此空间存在的静电场可能是( )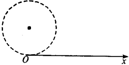 (2011?天门模拟)真空中有一半径为r的圆柱形匀强磁场区域,磁场方向垂直于纸面向里,Ox为过边界上O点的切线,如图所示.从O点在纸面内向各个方向发射速率均为V0的电子,设电子间相互作用忽略,且电子在磁场中的偏转半径也为r.已知电子的电荷量为e,质量为m.
(2011?天门模拟)真空中有一半径为r的圆柱形匀强磁场区域,磁场方向垂直于纸面向里,Ox为过边界上O点的切线,如图所示.从O点在纸面内向各个方向发射速率均为V0的电子,设电子间相互作用忽略,且电子在磁场中的偏转半径也为r.已知电子的电荷量为e,质量为m.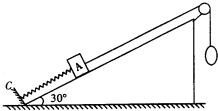 (2011?天门模拟)如图所示,在倾角为30°的光滑斜面上,一劲度系数为k的轻质弹簧一端固定在固定挡板C上,另一端连接一质量为m的物体A,一轻细绳通过定滑轮,一端系在物体A上,另一端有一细绳套,细绳与斜面平行,物体A处于静止状态.现在细绳套上轻轻挂上一个质量也为m的物体B,A将在斜面上做简谐运动.试求:
(2011?天门模拟)如图所示,在倾角为30°的光滑斜面上,一劲度系数为k的轻质弹簧一端固定在固定挡板C上,另一端连接一质量为m的物体A,一轻细绳通过定滑轮,一端系在物体A上,另一端有一细绳套,细绳与斜面平行,物体A处于静止状态.现在细绳套上轻轻挂上一个质量也为m的物体B,A将在斜面上做简谐运动.试求: