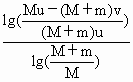Question

一个质量为M的雪橇静止在水平雪地上，一条质量为m的爱斯基摩狗站在该雪橇上．狗向雪橇的正后方跳下，随后又追赶并向前跳上雪橇；其后狗又反复地跳下、追赶并跳上雪橇，狗与雪橇始终沿一条直线运动．若狗跳离雪橇时雪橇的速度为V，则此时狗相对于地面的速度为V＋u(其中u为狗相对于雪橇的速度，V＋u为代数和．若以雪橇运动的方向为正方向，则V为正值，u为负值)．设狗总以速度v追赶和跳上雪橇，雪橇与雪地间的摩擦忽略不计．已知v的大小为5 m/s，u的大小为4 m/s，M＝30 kg，m＝10 kg. (1) 求狗第一次跳上雪橇后两者的共同速度的大小． (2) 求雪橇最终连度的大小和狗最多能跳上雪橇的次数． (供使用但不一定用到的对数值：lg2＝0.301，lg3＝0.477)

Answer 1

答案：
解析：

(1)

设雪橇反动的方向为正方向，狗第1次跳下雪橇后雪橇的速度为V1，根据动量守恒定律有MV1＋m(V1＋u)＝0 　　狗第1次跳上雪橇时，雪橇与狗的共同速度为1满足MV1＋mv＝(M＋m) 1，可解得 　　将u＝－4 m/s,v＝5 m/s,M＝30 kg,m＝10 kg代入，得1＝2 m/s

(2)

解法(1)：设雪橇运动的方向为正方向，狗第(n－1)次跳下雪橇后雪橇的速度为Vn－1，则狗第(n－1)次跳上雪橇后的速度n－1满足MVn－1＋mv＝(M＋m)n－1 　　这样，狗n次跳下雪橇后，雪橇的速度为Va满足MVa＋m(Vn＋u)＝(M＋m)n－1 　　解得Va＝(v－u)［1－()a－1］－ 　　狗追不上雪橇的条件是Va≥v 　　可化为()a－1≤ 　　最后可求得n≥1＋ 　　代入数据，得n≥3.41 　　狗最多能跳上雪橇3次，雪橇最终的速度大小为V 4＝5.625 m/s 　　解法(2)：设雪橇运动的方向为正方向，狗第i次跳下雪橇后，雪橇的速度为Vi，狗的速度为Vi+u；由动量守恒定律可得 　　第一次跳下雪橇：MV1＋m(V1＋u)＝0，V1＝－＝1 m/s 　　第一次跳上雪橇：MV1＋mv＝(M＋m)1 　　第二次跳下雪橇：(M＋m)1＝MV2＋m(V2＋u) V2＝＝3 m/s 　　第二次跳上雪橇：MV2＋mv＝(M＋m)V′2 　　2＝ 　　第三次跳下雪橇：(M＋m) 2＝MV3＋m(V3＋u) 　　V3＝4.53 m/s 　　第三次跳上雪橇： 　　(M＋m)V3＝V3＋m(3＋u) 　　3＝ 　　第四次跳下雪橇： 　　(M＋m)3＝MV4＋m(V4＋u) 　　V4＝＝5.625 m/s 　　此时雪橇的速度已大于狗追赶的速度，狗将不可能追上雪橇．因此，狗最多能跳上雪橇3次，雪橇最终的速度大小为5.625 m/s