题目内容
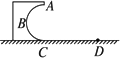
如图所示，一固定在竖直平面内的光滑半圆形轨道ABC，其半径R＝0.5 m，轨道在C处与水平地面相切．在C处放一小物块，给它一个水平向左的初速度v0＝5 m/s，结果它沿CBA运动，通过A点，最后落在水平地面上的D点，求C、D间的距离s．取重力加速度g＝10 m/s2．
答案：
解析：
解析：
|
本题考查机械能守恒定律，平抛运动等知识．可由机械能守恒定律计算出小物块到达A点的速度，再由平抛运动规律计算出CD间的距离． 设小物块的质量为m，过A处的速度为v，由A点到D点的时间为t．小物块从C到A过程，取水平地面为参考平面，由机械能守恒定律得 小物块过A点后做平抛运动，由 2R＝ s＝v0t 由以上各式联立，得 CD之间的距离为：s＝1 m． |
mv02＝
练习册系列答案
53随堂测系列答案
相关题目
（2006?甘肃）如图所示，一固定在竖直平面内的光滑的半圆形轨道ABC，其半径R=0.5m，轨道在C处与水平地面相切，在C处放一小物块，给它一水平向左的初速度v0=5m/s，结果它沿CBA运动，通过A点，最后落在水平地面上的D点，求C、D间的距离x．取重力加速度g=10m/s2．
如图所示，一固定在竖直平面内的光滑半圆形轨道ABC在C处与水平地面相切，轨道半径R=0.5m．在与C相距x=3m的O点放一小物体，物体与水平面问的动摩擦因数μ=0.4． 现给物体一水平向左的初速度v0，结果它沿OCBA 运动通过A点，最后落在水平地面上的D点（图中未画出），C、D问的距离s=l m，求物体的初速度秒v0的大小．（取重力加速度g=l0m/s2）
如图所示，一固定在竖直平面内的光滑的半圆形轨道ABC，其半径R=0.5m，轨道在C处与水平地面相切．在C处放一小物块，给它一水平向左的初速度，结果它沿CBA运动，小物块恰好能通过最高点A，最后落在水平面上的D点，（取g=10m/s2）求：
如图所示，一固定在竖直平面内的光滑的半圆形轨道ABC，其半径R=2.5m，轨道在C处与水平地面相切．在C处放一小球，给它一水平向左的初速度，结果它沿CBA运动，恰能通过A点，最后落在水平面上的D点，（g取10m/s2）
如图所示，一固定在竖直平面内的光滑的半圆形轨道ABC，其半径R=0.5m，轨道在C处与水平地面相切．在C处放一质量m=1kg的小物块，给它一水平向左的初速度v0=5m/s，结果它沿CBA运动，通过最高点A点后落在水平面上．求：