题目内容
9. 质量为M=3kg平板车放在光滑的水平面上,在平板车的最左端有一小物块(可视为质点),物块的质量为m=1kg,平板车与小物块间的动摩擦因数为μ=0.5,小车左端上方如图固定着一障碍物A,如图所示,初始时,平板车与物块一起以水平速度v0=2m/s向左运动,当物块运动到障碍物A处时与A发生无机械能损失的碰撞,而小车可继续向左运动.取重力加速度g=10m/s2.
质量为M=3kg平板车放在光滑的水平面上,在平板车的最左端有一小物块(可视为质点),物块的质量为m=1kg,平板车与小物块间的动摩擦因数为μ=0.5,小车左端上方如图固定着一障碍物A,如图所示,初始时,平板车与物块一起以水平速度v0=2m/s向左运动,当物块运动到障碍物A处时与A发生无机械能损失的碰撞,而小车可继续向左运动.取重力加速度g=10m/s2.(1)设平板车足够长,求物块与障碍物第一次碰撞后,物块与平板车所能获得的共同速率;
(2)要使物块不会从平板车上滑落,平板车至少应为多长?
(3)若物块未从平板车上滑落,求小物块与障碍物A第四次碰撞到第五次碰撞过程中,小物块经过的路程?
分析 (1)物块与障碍物碰后物块和小车系统动量守恒,根据动量守恒定律求出物块与障碍物第一次碰撞后,物块与平板车所能获得的共同速率.
(2)物块多次与障碍物碰撞后,最终与平板车同时停止.根据能量守恒定律求出平板车的最小长度.
(3)根据动量守恒定律求出第三次碰撞后的速度,抓住第四次碰撞后,小物块先向右做匀减速直线运动到零,再向左做匀加速,最终匀速,结合牛顿第二定律和运动学公式求出小物块通过的路程.
解答 解:(1)物块和障碍物碰后,物块和小车系统动量守恒,规定向左为正方向,有:Mv0-mv0=(M+m)v,
代入数据解得v=1m/s.
(2)物块多次与障碍物碰后,最终与平板车同时停止,设物块在平板车上运动的距离为l,那么由系统能量守恒有:
$μmgl=\frac{1}{2}(m+M){{v}_{0}}^{2}$,
代入数据解得l=1.6m.
所以要使物块不滑出平板车,平板车长度至少为1.6m.
(3)物块第一次与障碍物碰后向右减速到零再向左加速直到再次与平板车达到高速,规定向左为正方向,根据动量守恒有:
Mv0-mv0=(M+m)v1,
得${v}_{1}=\frac{{v}_{0}}{2}$,
物块第二次与障碍物碰后向右减速到零再向左加速直到再次与平板车达到共速,规定向左为正方向,根据动量守恒有:
Mv1-mv1=(M+m)v2,
解得${v}_{2}=\frac{1}{2}{v}_{1}=\frac{{v}_{0}}{4}$,
易得第三次碰撞后达到共同速度为${v}_{3}=\frac{{v}_{0}}{8}=0.25m/s$,
第四次碰撞后,小物块将以0.25m/s的速度,a=-μg=-5m/s2的加速度向右做匀减速直线运动到0,再向左先加速再匀速,
所以小物块与A第四次到第五次碰撞过程中,小物块经过的路程S=$\frac{{{v}_{3}}^{2}}{2a}×2=\frac{0.2{5}^{2}}{2×5}×2$m=0.0125m.
答:(1)物块与障碍物第一次碰撞后,物块与平板车所能获得的共同速率为1m/s;
(2)要使物块不会从平板车上滑落,平板车至少应为1.6m;
(3)小物块与障碍物A第四次碰撞到第五次碰撞过程中,小物块经过的路程为0.0125m.
点评 本题综合考查了动能定理、动量守恒定律和能量守恒定律,综合性较强,对学生能力要求较高,需加强这方面的训练.

 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
| A. | 交流220V | B. | 直流220V | C. | 交流4-6V | D. | 直流4-6V |
| A. | 平抛运动是曲线运动,它的速度方向不断改变,不可能是匀变速运动 | |
| B. | 平抛运动可以分解为水平方向的匀速直线运动和竖直方向的自由落体运动 | |
| C. | 平抛运动的落地时间与初速度大小无关 | |
| D. | 平抛运动的水平位移与抛出点的高度有关 |
 如图所示,两轮用皮带传动,假设皮带不打滑,图中A、B、C三点所处半径rA>rB=rC,则这三点的线速度、角速度的大小关系正确的是( )
如图所示,两轮用皮带传动,假设皮带不打滑,图中A、B、C三点所处半径rA>rB=rC,则这三点的线速度、角速度的大小关系正确的是( )| A. | vA=vB<vC | B. | vA=vB>vC | C. | wC=wA>wB | D. | wB>wA=wC |
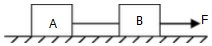
| A. | F2=F1 | B. | F1>F2 | C. | F2>F1 | D. | F1=μF2 |
 如图所示,一轻弹簧的下端固定在水平面上,弹簧处于原长状态,在其上端轻放一物体(物体与弹簧不连接),当物体下降到某一高度时,其速度恰好变为零.空气阻力不计,弹簧一直在弹性限度内.在物体接触弹簧至弹簧压缩到最短的过程中( )
如图所示,一轻弹簧的下端固定在水平面上,弹簧处于原长状态,在其上端轻放一物体(物体与弹簧不连接),当物体下降到某一高度时,其速度恰好变为零.空气阻力不计,弹簧一直在弹性限度内.在物体接触弹簧至弹簧压缩到最短的过程中( )| A. | 物体的动能一直增大 | B. | 物体的动能一直减小 | ||
| C. | 弹簧的弹性势能一直增大 | D. | 弹簧的弹性势能一直减小 |
| A. | 物体A在一定做加速运动 | B. | 物体A的加速度大于物体B的加速度 | ||
| C. | 物体B的加速度大于物体A的加速度 | D. | 物体A的速度小于B物体速度 |
 如图所示,一电阻为R的导线折成长为a的等边三角形闭合回路.虚线MN右侧有磁感应强度为B0的匀强磁场,方向垂直于回路所在的平面.回路以速度V向右匀速进入磁场,BC边始终与MN垂直.从C点进入磁场开始到B点进入磁场为止,下列结论正确的是( )
如图所示,一电阻为R的导线折成长为a的等边三角形闭合回路.虚线MN右侧有磁感应强度为B0的匀强磁场,方向垂直于回路所在的平面.回路以速度V向右匀速进入磁场,BC边始终与MN垂直.从C点进入磁场开始到B点进入磁场为止,下列结论正确的是( )| A. | A点到达磁场边界时感应电流方向发生改变 | |
| B. | BC边始终不受安培力作用 | |
| C. | 感应电动势平均值为$\frac{\sqrt{3}}{4}$B0aV | |
| D. | 通过导线横截面的电荷量为$\frac{\sqrt{3}{B}_{0}{a}^{2}}{4R}$ |
