题目内容
如图所示,物体的质量为2kg,两根轻细绳AB和AC的一端固定于竖直墙上,另一端系于物体上(∠BAC=θ=60°),在物体上另施加一个方向与水平线也成θ角的拉力F,若要使绳都能伸直,求拉力F的大小范围.


对A球受力分析,受到拉力F,重力mg,两根细绳的拉力FB、FC,如图所示,根据平衡条件,有:
x方向:Fcos60°=FC+FBcos60°
y方向:Fsin60°+FBsin60°=mg
解得:
FB=
mg-F
FC=F-
mg
当FB=0时,F最大,为:Fmax=
mg=
N;
当FC=0时,F最小,为:Fmin=
mg=
N;
故拉力F的范围为:
N≤F≤
N.
答:拉力F的大小范围为
N≤F≤
N

x方向:Fcos60°=FC+FBcos60°
y方向:Fsin60°+FBsin60°=mg
解得:
FB=
2
| ||
| 3 |
FC=F-
| ||
| 3 |
当FB=0时,F最大,为:Fmax=
2
| ||
| 3 |
| 40 |
| 3 |
| 3 |
当FC=0时,F最小,为:Fmin=
| ||
| 3 |
| 20 |
| 3 |
| 3 |
故拉力F的范围为:
20
| ||
| 3 |
40
| ||
| 3 |
答:拉力F的大小范围为
20
| ||
| 3 |
40
| ||
| 3 |


练习册系列答案
相关题目







 ,现在保持A读数不变化,减小
,现在保持A读数不变化,减小 角,要使结点仍在O处,可采用的办法是( )
角,要使结点仍在O处,可采用的办法是( )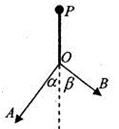
 角
角