题目内容
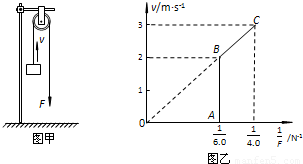
如图甲所示,某同学用轻绳通过定滑轮提升一重物,运用传感器(未在图中画出)测得此过程中不同时刻被提升重物的速度v与对轻绳的拉力F,并描绘出v-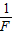 图象.假设某次实验所得的图象如图乙所示,其中线段AB与纵轴平行,它反映被提升重物在第一个时间段内v和1/F的关系;线段BC反映被提升重物在第二个时间段内v和
图象.假设某次实验所得的图象如图乙所示,其中线段AB与纵轴平行,它反映被提升重物在第一个时间段内v和1/F的关系;线段BC反映被提升重物在第二个时间段内v和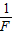 的关系,它的延长线过原点;第三个时间段内拉力F和速度v均为C点所对应的大小保持不变,因此图象上没有画出.实验中还测得重物由静止开始经过t=1.4s,速度增加到vC=3.0m/s,此后物体做匀速运动.取重力加速度g=10m/s2,绳重及一切摩擦力和阻力均忽略不计.试求:
的关系,它的延长线过原点;第三个时间段内拉力F和速度v均为C点所对应的大小保持不变,因此图象上没有画出.实验中还测得重物由静止开始经过t=1.4s,速度增加到vC=3.0m/s,此后物体做匀速运动.取重力加速度g=10m/s2,绳重及一切摩擦力和阻力均忽略不计.试求:(1)物体质量和第一个时间段内的时间.
(2)力F的最大功率.
(3)第二阶段内物体重力势能的变化量.
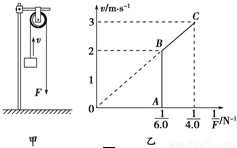
【答案】分析:(1)由v- 图象可知,重物速度达到vC=3.0 m/s时,受平衡力,由此解得重物的质量,第一个时间段内重物所受拉力保持不变,根据牛顿第二定律求出加速度,根据速度时间关系即可求得时间;
图象可知,重物速度达到vC=3.0 m/s时,受平衡力,由此解得重物的质量,第一个时间段内重物所受拉力保持不变,根据牛顿第二定律求出加速度,根据速度时间关系即可求得时间;
(2)由v- 图象可知从第二段时间开始,拉力与速度的乘积不变,即功率不变,即可求解;
图象可知从第二段时间开始,拉力与速度的乘积不变,即功率不变,即可求解;
(3)因从第二段时间开始P不变,根据动能定理及重物重力势能的变化量等于负的重力所做的功即可解题.
解答:解:(1)由v- 图象可知,重物速度达到vC=3.0 m/s时,受平衡力,
图象可知,重物速度达到vC=3.0 m/s时,受平衡力,
即G=F2=4.0 N.由此解得重物的质量m= =0.40 kg
=0.40 kg
第一个时间段内重物所受拉力保持不变,且F1=6.0 N
设其大小为a,根据牛顿第二定律有F1-G=ma 解得a=5.0 m/s2
设第一段时间为t1,重物在这段时间内的位移为s1,则
t1= =
= s=0.40 s
s=0.40 s
(2)由v- 图象可知从第二段时间开始,拉力与速度的乘积不变,即功率不变,则:
图象可知从第二段时间开始,拉力与速度的乘积不变,即功率不变,则:
P=Fv=12 W.
(3)因从第二段时间开始P不变,则根据动能定理有:Pt2-WG= m
m
而:t2=t-t1=1.0 s
所以重物重力势能的变化量△EP=-WG=11J
答:(1)物体质量和第一个时间段内的时间为0.40 s.
(2)力F的最大功率为12W;
(3)第二阶段内物体重力势能的变化量为11J.
点评:本题主要考查了动能定理及牛顿第二定律的应用,要能根据图象得出有效信息,难度适中.
 图象可知,重物速度达到vC=3.0 m/s时,受平衡力,由此解得重物的质量,第一个时间段内重物所受拉力保持不变,根据牛顿第二定律求出加速度,根据速度时间关系即可求得时间;
图象可知,重物速度达到vC=3.0 m/s时,受平衡力,由此解得重物的质量,第一个时间段内重物所受拉力保持不变,根据牛顿第二定律求出加速度,根据速度时间关系即可求得时间;(2)由v-
 图象可知从第二段时间开始,拉力与速度的乘积不变,即功率不变,即可求解;
图象可知从第二段时间开始,拉力与速度的乘积不变,即功率不变,即可求解;(3)因从第二段时间开始P不变,根据动能定理及重物重力势能的变化量等于负的重力所做的功即可解题.
解答:解:(1)由v-
 图象可知,重物速度达到vC=3.0 m/s时,受平衡力,
图象可知,重物速度达到vC=3.0 m/s时,受平衡力,即G=F2=4.0 N.由此解得重物的质量m=
 =0.40 kg
=0.40 kg 第一个时间段内重物所受拉力保持不变,且F1=6.0 N
设其大小为a,根据牛顿第二定律有F1-G=ma 解得a=5.0 m/s2
设第一段时间为t1,重物在这段时间内的位移为s1,则
t1=
 =
= s=0.40 s
s=0.40 s(2)由v-
 图象可知从第二段时间开始,拉力与速度的乘积不变,即功率不变,则:
图象可知从第二段时间开始,拉力与速度的乘积不变,即功率不变,则:P=Fv=12 W.
(3)因从第二段时间开始P不变,则根据动能定理有:Pt2-WG=
 m
m
而:t2=t-t1=1.0 s
所以重物重力势能的变化量△EP=-WG=11J
答:(1)物体质量和第一个时间段内的时间为0.40 s.
(2)力F的最大功率为12W;
(3)第二阶段内物体重力势能的变化量为11J.
点评:本题主要考查了动能定理及牛顿第二定律的应用,要能根据图象得出有效信息,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 (2010?长沙县模拟)如图甲所示,某同学用轻绳通过定滑轮提升一重物,运用传感器(未在图中画出)测得此过程中不同时刻被提升重物的速度v与对轻绳的拉力F,并描绘出v-
(2010?长沙县模拟)如图甲所示,某同学用轻绳通过定滑轮提升一重物,运用传感器(未在图中画出)测得此过程中不同时刻被提升重物的速度v与对轻绳的拉力F,并描绘出v-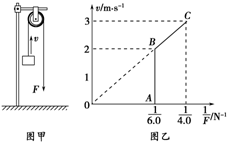 如图甲所示,某同学用轻绳通过定滑轮提升一个重物,运用传感器(未在图中画出)测得此过程中不同时刻被提升重物的速度v与对轻绳的拉力F,并描绘出v-
如图甲所示,某同学用轻绳通过定滑轮提升一个重物,运用传感器(未在图中画出)测得此过程中不同时刻被提升重物的速度v与对轻绳的拉力F,并描绘出v-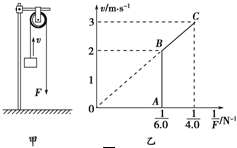 如图甲所示,某同学用轻绳通过定滑轮提升一重物,运用传感器(未在图中画出)测得此过程中不同时刻被提升重物的速度v与对轻绳的拉力F,并描绘出v-
如图甲所示,某同学用轻绳通过定滑轮提升一重物,运用传感器(未在图中画出)测得此过程中不同时刻被提升重物的速度v与对轻绳的拉力F,并描绘出v-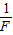 图象.假设某次实验所得的图象如图乙所示,其中线段AB与v轴平行,它反映了被提升重物在第一个时间段内v和
图象.假设某次实验所得的图象如图乙所示,其中线段AB与v轴平行,它反映了被提升重物在第一个时间段内v和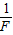 的关系;线段BC的延长线过原点,它反映了被提升重物在第二个时间段内v和
的关系;线段BC的延长线过原点,它反映了被提升重物在第二个时间段内v和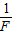 的关系;第三个时间段内拉力F和速度v均为C点所对应的大小保持不变,因此图象上没有反映.实验中还测得重物由静止开始经过t=1.4s,速度增加到vC=3.0m/s,此后物体做匀速运动.取重力加速度g=10m/s2,绳重及一切摩擦和阻力均可忽略不计.
的关系;第三个时间段内拉力F和速度v均为C点所对应的大小保持不变,因此图象上没有反映.实验中还测得重物由静止开始经过t=1.4s,速度增加到vC=3.0m/s,此后物体做匀速运动.取重力加速度g=10m/s2,绳重及一切摩擦和阻力均可忽略不计.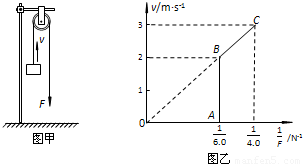
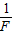 图象.假设某次实验所得的图象如图乙所示,其中线段AB与v轴平行,它反映了被提升重物在第一个时间段内v和
图象.假设某次实验所得的图象如图乙所示,其中线段AB与v轴平行,它反映了被提升重物在第一个时间段内v和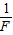 的关系;线段BC的延长线过原点,它反映了被提升重物在第二个时间段内v和
的关系;线段BC的延长线过原点,它反映了被提升重物在第二个时间段内v和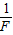 的关系;第三个时间段内拉力F和速度v均为C点所对应的大小保持不变,因此图象上没有反映.实验中还测得重物由静止开始经过t=1.4s,速度增加到vC=3.0m/s,此后物体做匀速运动.取重力加速度g=10m/s2,绳重及一切摩擦和阻力均可忽略不计.
的关系;第三个时间段内拉力F和速度v均为C点所对应的大小保持不变,因此图象上没有反映.实验中还测得重物由静止开始经过t=1.4s,速度增加到vC=3.0m/s,此后物体做匀速运动.取重力加速度g=10m/s2,绳重及一切摩擦和阻力均可忽略不计.