题目内容
如图是一根轻质细绳拴在两悬崖间,悬点等高,特种兵利用动滑轮在细绳上从一端滑向另一端,已知特种兵的质量为m,特种兵滑到最低点时绳与水平方向夹角为θ,不计动滑轮重力和动滑轮与绳间的摩擦,则在最低点绳中的张力F为( )
A.F=

B.F=

C.F

D.F

【答案】分析:特种兵滑到最低点时具有向上的加速度,由绳子的拉力和重力的合力提供向心力,由牛顿第二定律求出F的大小.
解答:解:设特种兵滑到最低点时所受的绳子拉力大小为F′,不计动滑轮重力和动滑轮与绳间的摩擦,则有:
2Fsinθ=F′,
此时,特种兵具有向上的加速度,由牛顿第二定律得知,其合力向上,则:F′>mg
即有:2Fsinθ>mg
解得:F> ,所以选项ABC错误,D正确.
,所以选项ABC错误,D正确.
故选D
点评:本题关键要抓住特种兵滑到最低点时具有向上的加速度,由牛顿第二定律和力的合成进行分析.
解答:解:设特种兵滑到最低点时所受的绳子拉力大小为F′,不计动滑轮重力和动滑轮与绳间的摩擦,则有:
2Fsinθ=F′,
此时,特种兵具有向上的加速度,由牛顿第二定律得知,其合力向上,则:F′>mg
即有:2Fsinθ>mg
解得:F>
 ,所以选项ABC错误,D正确.
,所以选项ABC错误,D正确.故选D
点评:本题关键要抓住特种兵滑到最低点时具有向上的加速度,由牛顿第二定律和力的合成进行分析.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
 如图是一根轻质细绳拴在两悬崖间,悬点等高,特种兵利用动滑轮在细绳上从一端滑向另一端,已知特种兵的质量为m,特种兵滑到最低点时绳与水平方向夹角为θ,不计动滑轮重力和动滑轮与绳间的摩擦,则在最低点绳中的张力F为( )
如图是一根轻质细绳拴在两悬崖间,悬点等高,特种兵利用动滑轮在细绳上从一端滑向另一端,已知特种兵的质量为m,特种兵滑到最低点时绳与水平方向夹角为θ,不计动滑轮重力和动滑轮与绳间的摩擦,则在最低点绳中的张力F为( ) 如图是一根轻质细绳拴在两悬崖间,悬点等高,特种兵利用动滑轮在细绳上从一端滑向另一端,已知特种兵的质量为m,特种兵滑到最低点时绳与水平方向夹角为θ,不计动滑轮重力和动滑轮与绳间的摩擦,则在最低点绳中的张力F为
如图是一根轻质细绳拴在两悬崖间,悬点等高,特种兵利用动滑轮在细绳上从一端滑向另一端,已知特种兵的质量为m,特种兵滑到最低点时绳与水平方向夹角为θ,不计动滑轮重力和动滑轮与绳间的摩擦,则在最低点绳中的张力F为
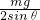










 =
= 
















